Принадлежность точки поверхности (A ∈ α)
ТеорияПри составлении алгоритма решения этой группы задач следует базироваться на свойстве (3) из § 38, т. е. для того чтобы на чертеже поверхности указать проекции принадлежащей ей точки, необходимо вначале построить проекции какой-либо линии, принадлежащей поверхности, а затем на этой линии отметить точку.
В качестве линии, как правило, выбирается образующая поверхности. Если поверхность может быть получена образующей различной формы, то предпочтение следует отдавать наиболее простым и удобным для построения линиям: окружностям для поверхностей вращения, прямым для линейчатых поверхностей (в частности, для плоскости целесообразно использовать линии уровня *).
ПРИМЕР 1. В плоскости α (а || b) указать произвольную точку A (рис. 169).
РЕШЕНИЕ. В плоскости α проводим произвольную горизонталь h. При построении ее проекций следует иметь в виду, что прямая принадлежит плоскости в том случае, если она содержит две различные точки, принадлежащие плоскости. В качестве таких точек принимаем точки 1 и 2, принадлежащие соответственно прямым а и b, определяющим плоскость α.
На рис. 169 построение проекций горизонтали h выполнено и следующей последовательности:
а) на прямой а взяли произвольную точку 1, через фронтальную проекцию этой точки провели фронтальную проекцию горизонтали h";
б) отметили точку 2" = h" ∩ b";
в) определили горизонтальные проекции 1' и 2' точек 1 и 2;
г) через точки 1' и 2' провели горизонтальную проекции горизонтали h' .
Горизонталь h ⊂ α, так как h проходит через точки 1 и 2, принадлежащие плоскости α
* Особенно целесообразно пользоваться линиями уровня в случае, когда плоскость задана следами.
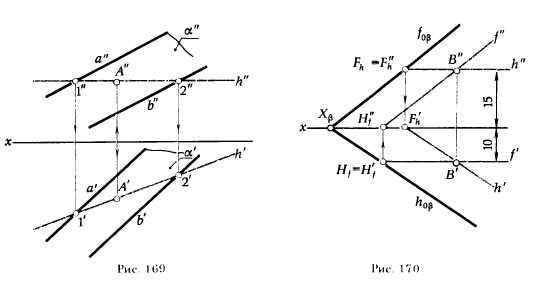
На проекциях горизонтали h' и h" отмечаем проекции точки A (A' ∈ h' и A" ∈ h"). Точка A ⊂ α, так как A ∈ l ⊂ α.
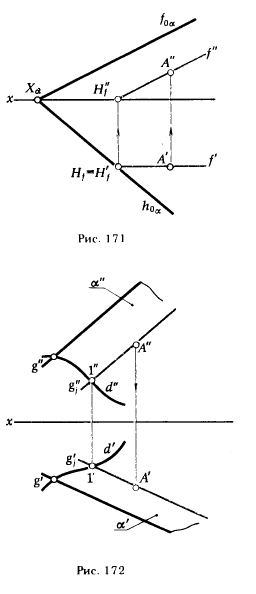
ПРИМЕР 2. В плоскости β указать точку В, удаленную от горизонтальной плоскости проекции на расстояние 15 мм и от фронтальной плоскости проекции на расстояние 10 мм (рис. 170) .
РЕШЕНИЕ. Проводим в плоскости β фронталь f и горизонталь h, удаленные от плоскостей проекций соответственно на расстояния 10 и 15 мм. Пересечение одноименных проекций f и h укажет проекции искомой точки В (В' = f' ∩ h' , В" = f" ∩ h").
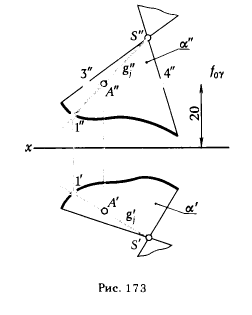
ПРИМЕР 3. Определить фронтальную проекцию точки A, принадлежащей плоскости α, если известна ее горизонтальная проекция А' (рис. 171).
Мы знаем, что А ∈ α ⇐⇒ (A' ∈ l' ⊂ α') ∧ (A" ∈ l" ⊂ α"), позтому, чтобы получить ответ на поставленную задачу, достаточно через A' провести горизонтальную проекцию прямой, принадлежащей плоскости α, найти ее фронтальную проекциию и на ней отметить точку A" .Так как плоскость α задана следами, то целесообразно в качестве вспомогательной прямой использовать одну из главных линий плоскости. На рис. 171 проведена фронталь f плоскости α.
ПРИМЕР 4. На цилиндрической поверхности α, заданной направляющей d и образующей g, указать произвольную точку A (рис. 172).
РЕШЕНИЕ. Проводим произвольную прямолинейную образующую gj цилиндрической поверхности α. Для зтого на кривой d отмечаем произвольную точку l(l' ∈ d' и l" ∈ d") . Через проекции точки l проводим проекции прямой gj параллельно соответствующим проекциям g' и g". На прямой gj отмечаем произвольную точку А: A ∈ α ⇐⇒ (A'∈ g'j ⊂ α') ∧ (A" ∈ g"j ⊂ α").
ПРИМЕР 5. На конической поверхности α указать точку А, удаленную от горизонтальной плоскости проекции на расстояние 20 мм (рис. 17 3).
РЕШЕНИЕ. Проводим плоскость γ || π1 и удаленную от оси х на заданное расстояние 20 мм. На конической поверхности а отмечаем произвольную прямолинейную образующую gj (g'j, g"j.). Точка пересечения g"j ∩ f0γ укажет фронтальную проекцию А" искомой точки А. По А" находим А'.
Следует иметь в виду, что данная задача имеет бесчисленное множество решений: любая точка отрезка 3", 4" может быть принята за фронтальную проекцию точки, удовлетворяющей условию поставленной задачи.
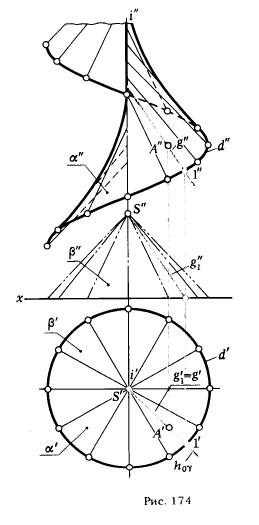
ПРИМЕР 6. На поверхности наклонного геликоида α: указать фронтальную проекцию точки А, если известна ее горизонтальная проекция А' (рис. 174).
РЕШЕНИЕ. Через горизонтальную проекцию точки А' проводим горизонтальную проекцию прямолинейной образующей g'. Фронтальная проекция g" определяется из условия равенства углов наклона всех прямолинейных образующих к направляющей плоскости (в нашем случае за направляющую плоскость при-нята π1 ).
Множество прямых, пересекающих ось винтовой поверхности i в точке S, образуют поверхность прямого кругового конуса β, прямолинейные образующие которого составляют заданный угол с плоскостью π1 . Поэтому для определения фронтальной проекции g" проводим прямолинейную образующую g1 конической поверхности β, по которой горизонтально проецирующая плоскость γ, проходящая через точку А и ось i, пересекает поверхность β. Фронтальная проекция g" должна быть параллельна g"1. Для ее построения на горизонтальной проекции d' отмечаем точку 1', в которой h0γ ∩ d'- по 1' определяем 1". Через 1" проводим g" || g"1. Для построения фронтальной проекции А" через А' проводим линию связи перпендикулярно оси х и отмечаем точку ее пересечения с g".
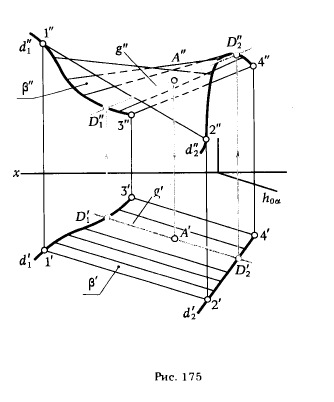
ПРИМЕР 7. На поверхности цилиндроида β указать фронтальную проекцию точки А, если известна ее горизонтальная проекция A' (рис. 175).
РЕШЕНИЕ. Через горизонтальную проекцию точки А' проводим горизонтальную проекцию прямолинейной образующей g' поверхности β, для зтого через A' проводим прямую g' || h0α и отмечаем точки D'1 и D'2, в которых прямая g' пересекает направляющие d'1 и d'2 .
По точкам D'1 и D'2 строим их фронтальные проекции D"1 и D"2, которые определяют фронтальную проекцию образующей g". На g" находим точку А". Для ее построения через А' проводим линию связи перпендикулярно оси х и отмечаем точку ее пересечения с g".
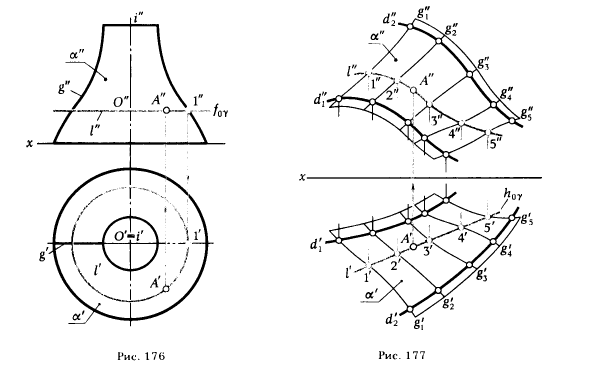
ПРИМЕР 8. Построить горизонтальную проекцию точки, принадлежащей поверхности вращения α(g, i), если известна ее фронтальная проекция А" (рис. 176) .
РЕШЕНИЕ. Через данную фронтальную проекцию точки А" проводим фронтальную проекцию окружности l" , принадлежащей поверхности α. Строим горизонтальную проекцию этой окружности l'. Окружность l - параллель поверхности α, ее следует рассматривать как сечение поверхности α горизонтальной плоскостью γ. Длина отрезка O"1" укажет величину радиуса окружности l'. На l' отмечаем А. Для нахождения А' через А" проводим линию связи перпендикулярно оси х и отмечаем точку ее пересечения с l'
В рассмотренных примерах были заданы поверхности линейчатые или вращения. Это позволило для решения задачи на принадлежность точки поверхности использовать простые линии - прямые или окружности. Для нелинейчатых поверхностей, на которых невозможно провести такие линии, приходится строить кривые, принадлежащие поверхности.
Приведенный ниже пример показывает, как следует решать задачу на принадлежность точки поверхности в случае, когда поверхность нелинейчатая.
ПРИМЕР 9. Определить недостающую (фронтальную) проекцию точки А, принадлежащей нелинейчатой поверхности α, если известна ее горизонтальная проекция А' (рис. 177) .
РЕШЕНИЕ. Определение недостающей проекции точки А осуществляется аналогично рассмотренным ранее случаям (см. примеры 1 ... 8). Вначале через точку А' проводим прямую l' - горизонтальную проекцию линии l. Чтобы линия l принадлежала поверхности α, необходимо, чтобы любые точки, взятые на этой линии, принадлежали поверхности α. В качестве таких точек принимаем точки 1', 2', 3',4', 5', в которых l' пересекает горизонтальные проекции образующих g'1, g'2, g'3, g'4, g'5; зная 1' , 2' , ... , 5', определяем 1" ,2",... , 5". Соединив эти точки плавной кривой, получим l"; на l" отмечаем А" .Точка A ∈ α, так как A' ∈ l' и A" ∈ l" ,а l ⊂ α.
Следует иметь в виду, что при решении подобных задач в качестве линии l целесообразно пользоваться плоской кривой, в частности, принадлежащей проецирующей плоскости (в рассмотренном случае кривая l принадлежит горизонтально проецирующей плоскости γ).