Определение расстояния между точкой и плоскостью, прямой и плоскостью, между плоскостями и скрещивающимися прямыми
ТеорияОпределение расстояния между: 1 - точкой и плоскостью; 2 - прямой и плоскостью; 3 - плоскостями; 4 - скрещивающимися прямыми рассматривается совместно, так как алгоритм решения для всех этих задач по существу одинаков и состоит из геометрических построений, которые нужно выполнить для определения расстояния между заданными точкой А и плоскостью α. Если и есть какое-то различие, то оно состоит лишь в том, что в случаях 2 и 3 прежде чем приступить к решению задачи, следует на прямой m (случай 2) или плоскости β (случай 3) отметить произвольную точку А. При определении расстояния между скрещивающимися прямыми предварительно заключаем их в параллельные плоскости α и β с последующим определением расстояния между этими плоскостями.
Рассмотрим каждый из отмеченных случаев решения задач.
1. Определение расстояния между точкой и плоскостью.
Расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, опущенного из точки на плоскость.
Поэтому решение этой задачи состоит из последовательного выполнения следующих графических операций:
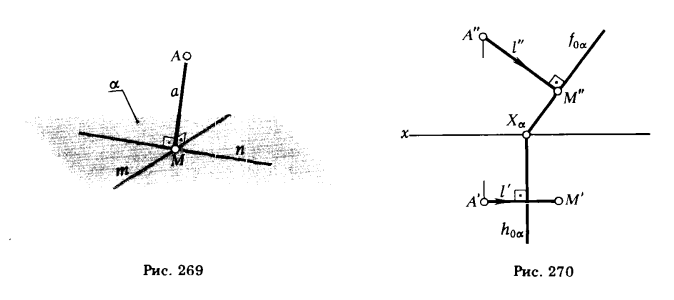
1) из точки А опускаем перпендикуляра на плоскость α (рис. 269);
2) находим точку М пересечения этого перпендикуляра с плоскостью М = а ∩ α;
3) определяем длину отрезка [AM].
Если плоскость α общего положения, то для того чтобы опустить на эту плоскость перпендикуляр, необходимо предварительно определить направление проекций горизонтали и фронтали этой плоскости. Нахождение точки встречи этого перпендикуляра с плоскостью также требует выполнения дополнительных геометрических построений.
Решение задачи упрощается, если плоскость α занимает частное положение относительно плоскостей проекций. В этом случае и проведение проекций перпендикуляра, и нахождение точки его встречи с плоскостью осуществляется без каких-либо дополнительных вспомогательных построений.
ПРИМЕР 1. Определить расстояние от точки А до фронтально проецирующей плоскости α (рис. 270).
РЕШЕНИЕ. Через А' проводим горизонтальную проекцию перпендикуляра l' ⊥ h0α, а через А" - его фронтальную проекцию l" ⊥ f0α. Отмечаем точку M" = l" ∩ f0α. Так как AM || π2, то [А" М"] == |АМ| = d.
Из рассмотренного примера видно, насколько просто решается задача, когда плоскость занимает проецирующее положение. Поэтому, если в исходных данных будет задана плоскость общего положения, то, прежде чем приступить к решению, следует перевести плоскость в положение, перпендикулярное к какой-либо плоскости проекции.
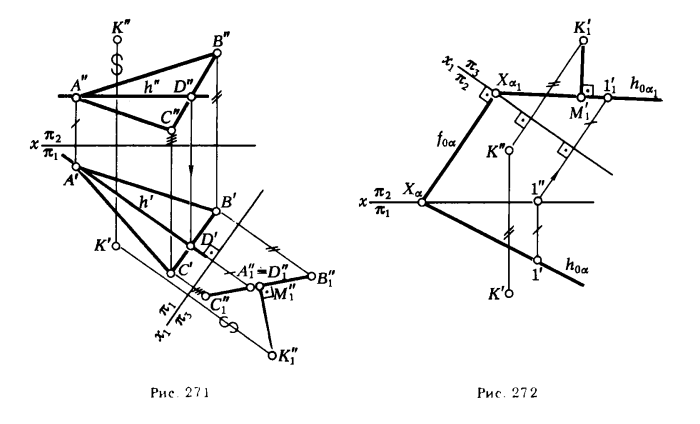
ПРИМЕР 2. Определить расстояние от точки К до плоскости, заданной ΔАВС (рис. 271).
РЕШЕНИЕ.
1. Переводим плоскость ΔАВС в проецирующее положение *. Для этого переходим от системы xπ2/π1 к x1π3/π1: направление новой оси х1 выбирается перпендикулярным к горизонтальной проекции горизонтали плоскости треугольника.
2. Проецируем ΔАВС на новую плоскость π3 (плоскость ΔАВС спроецируется на π3, в [ С"1В"1] ).
3. Проецируем на ту же плоскость точку К (К' → К"1).
4. Через точку К"1 проводим (К"1М"1 )⊥ отрезку [С"1В"1]. Искомое расстояние d = |K"1M"1| .
Решение задачи упрощается, если плоскость задана следами, так как отпадает необходимость в проведении проекций линий уровня.
ПРИМЕР 3. Определить расстояние от точки К до плоскости α, заданной следами (рис. 272) .
* Наиболее рациональным путем перевода плоскости треугольника в проецирующее положение является способ замены плоскостей проекций, так как в этом случае достаточно построить только одну вспомогательную проекцию.
РЕШЕНИЕ. Заменяем плоскость π1 плоскостью π3, для этого проводим новую ось x1 ⊥ f0α. На h0α отмечаем произвольную точку 1' и определяем ее новую горизонтальную проекцию на плоскости π3 (1'1). Через точки Xα1 (Хα1 = h0α1 ∩ x1 ) и 1'1 проводим h0α1. Определяем новую горизонтальную проекцию точки К → К'1. Из точки К'1 опускаем перпендикуляр на h0α1 и отмечаем точку его пересечения с h0α1 - М'1. Длина отрезка K'1M'1 укажет искомое расстояние.
2. Определение расстояния между прямой и плоскостью.
Расстояние между прямой и плоскостью определяется длиной отрезка перпендикуляра, опущенного из произвольной точки прямой на плоскость (см. рис. 248).
Поэтому решение задачи по определению расстояния между прямой m и плоскостью α ничем не отличается от рассмотренных в п. 1 примеров на определение расстояния между точкой и плоскостью (см. рис. 270 ... 272). В качестве точки можно брать любую точку, принадлежащую прямой m.
3.Определение расстояния между плоскостями.
Расстояние между плоскостями определяется величиной отрезка перпендикуляра, опущенного из точки, взятой на одной плоскости, на другую плоскость.
Из этого определения вытекает, что алгоритм решения задачи по нахождению расстояния между плоскостями α и β отличается от аналогичного алгоритма решения задачи по определению расстояния между прямой m и плоскостью α лишь тем, что прямая m должна принадлежать плоскости α, т. е., чтобы определить расстояние между плоскостями α и β, следует:
1) взять в плоскости α прямую m;
2) выделить на прямой m произвольную точку А;
3) из точки А опустить перпендикуляр l на плоскость β;
4) определить точку М - точку встречи перпендикуляра l с плоскостью β;
5) определить величину отрезка [AM] .
На практике целесообразно пользоваться другим алгоритмом решения, который будет отличаться от приведенного лишь тем, что, прежде чем приступить к выполнению первого пункта, следует перевести плоскости в проецирующее положение.
Включение в алгоритм этой дополнительной операции упрощает выполнение всех без исключения остальных пунктов, что, в конечном счете, приводит к более простому решению.
ПРИМЕР 1. Определить расстояние между плоскостями α и β (рис. 273).
РЕШЕНИЕ. Переходим от системы xπ2/π1 к x1π1/π3. По отношению к новой плоскости π3 плоскости α и β занимают проецирующее положение, поэтому расстояние между новыми фронтальными ,следами f0α1 и f0β1 является искомым.
В инженерной практике часто приходится решать задачу на построение плоскости, параллельной данной и удаленной от нее на заданное расстояние. Приведенный ниже пример 2 иллюстрирует решение такой задачи.
ПРИМЕР 2. Требуется построить проекции плоскости β, параллельной данной плоскости α (m || n), если известно, что расстояние между ними равно d (рис. 274).
РЕШЕНИЕ.
1. В плоскости α проводим произвольные горизонталь h (1, 3) и фронталь f (1,2).
2. Из точки 1 восставляем перпендикуляр l к плоскости α(l' ⊥ h', l" ⊥ f").
3. На перпендикуляре l отмечаем произвольную точку А.
4. Определяем длину отрезка [1А] - [1'А0] (положение [1'А0] указывает на эпюре метрически неискаженное направление прямой l).
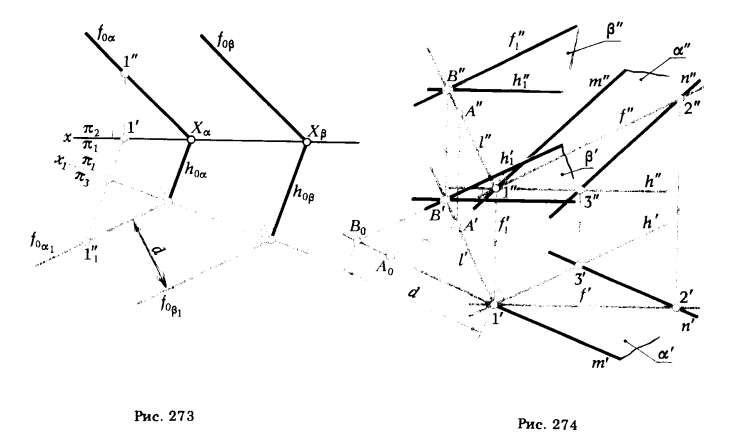
5. Откладываем на прямой (1'А0) от точки 1' отрезок [1'В0] = d.
6. Отмечаем на проекциях l' и l" точки В' и В", соответствующие точке В0.
7. Через точку В проводим плоскость β (h1 ∩ f1). Чтобы β || α, необходимо coблюдать условие h1 || h и f1 || f.
4. Определение расстояния между скрещивающимися прямыми.
Расстояние между скрещивающимися прямыми определяется длиной перпендикуляра, заключенного между параллельными плоскостями, которым принадлежат скрещивающиеся прямые.
Для того чтобы через скрещивающиеся прямые m и f провести взаимно параллельные плоскости α и β, достаточно через точку А (А ∈ m) провести прямую р, параллельную прямой f, а через точку В (В ∈ f) - прямую k, параллельную прямой m. Пересекающиеся прямые m и р, f и k определяют взаимно параллельные плоскости α и β (см. рис. 248, е). Расстояние между плоскостями α и β равно искомому расстоянию между скрещивающимися прямыми m и f.
Можно предложить и другой путь для определения расстояния между скрещивающимися прямыми, который состоит в том, что с помощью какого-либо способа преобразования ортогональных проекций одна из скрещивающихся прямых переводится в проецирующее положение. В этом случае одна проекция прямой вырождается в точку. Расстояние между новыми проекциями скрещивающихся прямых (точкой A'2 и отрезком C'2D'2) является искомым.
На рис. 275 приведено решение задачи на определение расстояния между скрещивающимися прямыми а и b, заданными отрезками [АВ] и [ CD]. Решение выполняют в следующей последовательности:
1. Переводят одну из скрещивающихся прямых (а) в положение, параллельное плоскости π3; для этого переходят от системы плоскостей проекции xπ2/π1 к новой x1π1/π3 , ось x1 проводят параллельно горизонтальной проекции прямой а . Определяют а"1 [А"1В"1] и b"1 [C"1D"1].
2. Путем замены плоскости π1 плоскостью π4 переводят прямую
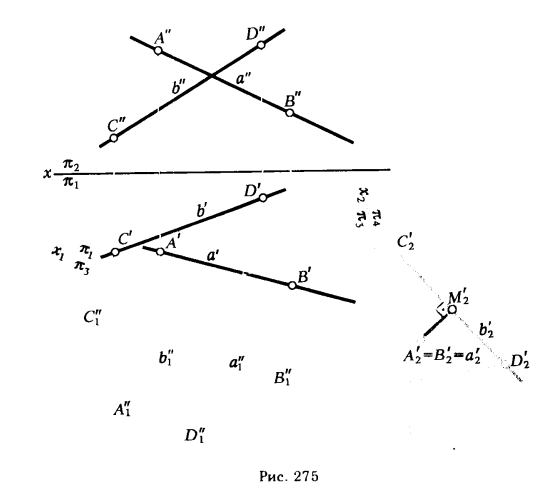
а в положение а'2, перпендикулярное плоскости π4 (новую ось х2 проводят перпендикулярно а"1).
3. Строят новую горизонтальную проекцию прямой b'2 - [ C'2D'2].
4. Расстояние от точки А'2 до прямой C'2D'2 ( отрезок ( А'2М'2] (является искомым.
Следует иметь в виду, что перевод одной из скрещивающихся прямых в проецирующее положение является ничем иным, как переводом плоскостей параллелизма, в которые можно заключить прямые а и b, также в проецирующее положение.
В самом деле, переведя прямую а в положение, перпендикулярное плоскости π4, мы обеспечиваем перпендикулярность любой плоскости, содержащей прямую а, плоскости π4, в том числе и плоскости α, определяемой прямыми а и m (а ∩ m, m || b). Если мы теперь проведем прямую n, параллельную а и пересекающую прямую b, то мы получим плоскость β, являющуюся второй плоскостью параллелизма, в которую заключены скрещивающиеся прямые а и b. Так как β || α, то и β ⊥ π4.