Пересечение призм и пирамид плоскостью и прямой линией

Для построения фигуры, получаемой при пересечении призмы и пирамиды плоскостью, надо или найти точки, в которых ребра призмы или пирамиды пересекают данную плоскость, или найти отрезки прямых, по которым грани призмы или пирамиды пересекаются плоскостью. В первом случае построение сводится к задаче на пересечение прямой с плоскостью, во втором случае — на пересечение плоскостей между собой.

В тех случаях, когда секущая плоскость не параллельна ни одной из плоскостей проекций, фигура сечения проецируется с искажением. Поэтому, если требуется определить натуральный вид фигуры сечения ¹), то следует применять один из способов, которые позволяют находить длину отрезка, величину угла и т. д. (см. главу V).

На рис. 273 показано пересечение прямой четырехугольной призмы плоскостью, заданной пересекающимися прямыми EF и EG. Обозначим эту плоскость буквой δ.

При пересечении получается четырехугольник, вершины которого представляют собой точки пересечения ребер призмы с пл.δ.Так как в данном случае призма прямая и основание ее параллельно пл. π₁, то горизонтальная проекция фигуры сечения определяется сразу, без какого-либо построения: она накладывается на проекцию A'B'C'D'. Очевидно, можно найти точки К и L, в которых ребра призмы, проходящие через точки А и D, пересекают пл. δ, при помощи одной пл. α, в которой находится грань призмы α × δ = 1—2, откуда получаем точки К" и L".Проведя" пл. β, получим β × δ = 3 — 4 и точки М' и N'.

¹) Выражение «натуральный вид сечения» мы будем применять в том случае, когда фигура сечения дается без искажения.

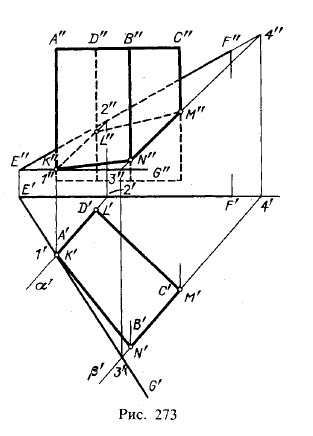
Итак, способ построения, который указан на рис. 273, сводится к применению вспомогательных плоскостей α и β, проходящих через соответствующие грани призмы, и построению отрезков KL и MN, по которым эти грани пересекаются пл. δ.

На фронтальной проекции линия пересечения состоит из видимой и невидимой частей; видимая часть линии пересечения расположена на обращенных к зрителю видимых гранях.

На рис. 273 находящаяся под пл. δ нижняя часть призмы представлена как невидимая. Линия пересечения лишь прочерчена на гранях призмы.

Если секущая плоскость перпендикулярна к одной из плоскостей проекций (рис. 274, слева), то проекции фигуры сечения получаются без каких-либо дополнительных проекция K"P"M"N" располагается на следе β", горизонтальная проекция K'P'N'M' совпадает с проекцией призмы.

На рис. 274 справа показано пересечение призмы пл. α, заданной пересекающимися прямыми АВ и ВМ₂, из которых ВМ₂ параллельна ребрам призмы. Следовательно, секущая плоскость в данном случае общего положения, параллельная

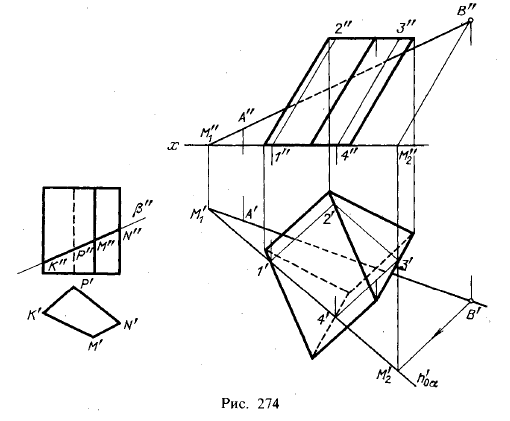
ребрам призмы. Она пересекает призмы по параллелограмму 1 — 2 — 3 — 4, стороны 1 — 2 и 3 — 4 которого параллельны ребрам призмы. Чтобы провести эти стороны, надо построить след пл. α на плоскости основания призмы и пересечь им это основание по прямой 1—4.

На рис. 275 показано пересечение пирамиды плоскостью общего положения α, выраженной следами. Дело сводится к нахождению точек пересечения ребер SA, SB и SC с пл. α, т. е. к задаче на пересечение прямой с плоскостью (см. § 25). Рассмотрим нахождение точки L, в которой ребро SB пересекает пл. α. Выполняем следующие действия: 1) через SB проводим вспомогательную плоскость, в данном случае горизонтально-проецирующую β; 2) находим прямую пересечения 1—2 плоскостей α и β; 3) находим точку L в пересечении прямых SB и 1 — 2.

Далее, так как в данном случае ребро SA расположено параллельно пл. π₂, проводим через него вспомогательную фронтальную плоскость δ. Она пересекает пл. α

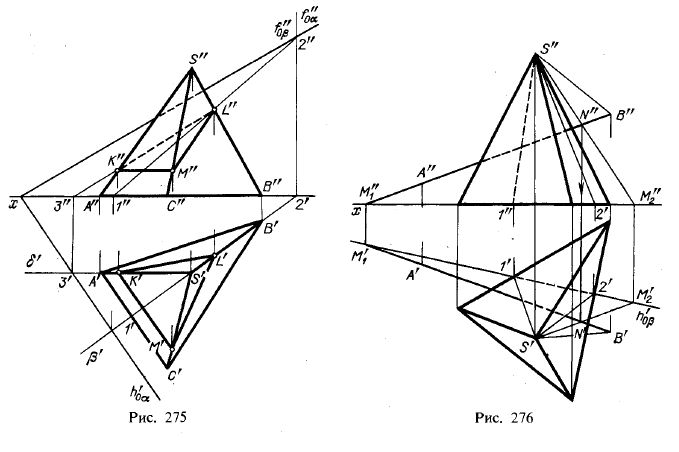
по ее фронтали с начальной точкой 3; в пересечении этой фронтали с ребром SA получаем точку К.

Теперь обратим внимание на другую особенность в данном примере: проекция А'С' параллельна следу h'_0α. Это тот случай, когда у двух плоскостей горизонтальные следы взаимно параллельны (h'_0α|| А'С', но А'С' — часть горизонтального следа плоскости грани SAC) и линия пересечения таких плоскостей является их общей горизонталью. Поэтому мы можем провести через уже найденную точку К прямую, параллельную ребру АС (или ||h'_0α, и так найти точку М.

Если бы не было этих особенностей, то следовало бы поступать аналогично построению точки L.

Чертеж на рис. 275 выполнен согласно условию, что пл. α прозрачна и что основным является нанесение на гранях линий разделения пирамиды на две части.

Пусть (рис. 276) пирамида рассечена пл. α, заданной пересекающимися прямыми АВ и SB, причем SB проходит через вершину пирамиды. Следовательно, пл. α рассекает ее по треугольнику, одна из вершин которого находится в точке S. Чтобы найти две другие вершины треугольника — точки 1 и 2, надо построить след пл. α на плоскости основания пирамиды. Остальное ясно из чертежа.

При пересечении поверхности призмы или пирамиды прямой линией получаются две точки. Для них встречается название точки входа и выхода. Чтобы найти эти точки, надо провести через данную прямую вспомогательную плоскость и найти линии ее пересечения с гранями; эти линии на гранях оказываются расположенными в одной плоскости с данной прямой и в своем пересечении дают точки, в которых данная прямая пересекает поверхность.

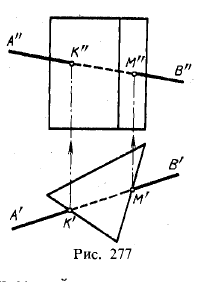
Могут быть случаи, когда нет надобности в таких построениях. Пример дан на рис. 277; положение проекций К' и М' очевидно, так как боковые грани призмы перпендикулярны к пл. π₁. По точкам К' и М' найдены точки К" и М".

На рис. 278 показано построение точек пересечения прямой линии с поверхностью пирамиды. Через прямую АВ проведена вспомогательная фронтально-проецирующая пл. α. Фронтальная проекция фигуры сечения пирамиды этой плоскостью сливается с фронтальной проекцией плоскости; горизонтальная проекция сечения найдена построением. Точки пересечения горизонтальной проекции прямой АВ с горизонтальной проекцией фигуры сечения представляют собой горизонтальные проекции искомых точек; по найденным горизонтальным проекциям (точки К' и М') построены фронтальные проекции (К" и М") точек пересечения.

----------

Построение точек пересечения прямой линии с поверхностью призмы можно представить себе еще следующим образом. Положим, что мы вместо прямоугольного проецирования применим косоугольное. Спроецируем призму и прямую АВ (рис. 279) на пл. π₁ по направлению, параллельному ребрам данной призмы. Призма спроецируется в треугольник C₁D₁E₁, совпадающий е горизонтальной

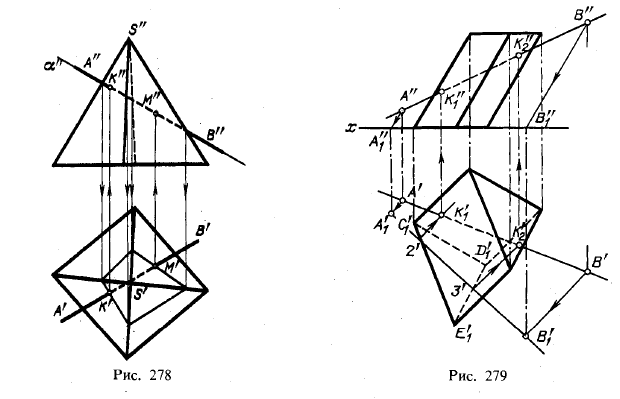
проекцией нижнего основания призмы, а прямая АВ — в прямую А₁В₁, которая пересечет стороны треугольника C₁D₁E₁ в точках 2 и 3. Обратным проецированием мы получим проекции К'₁ и К'₂, а по ним К"₁ и К"₂.

Итак, мы рассмотрели пересечение призм и пирамид плоскостью и прямой линией. Построения сводятся к решению задач на пересечение плоскостей и прямой с плоскостью, изложенных в §§ 24 — 26. Эти задачи имеют существенное значение и встречаются в различных случаях. Они же лежат в основе построения линий взаимного пересечения многогранных поверхностей, рассматриваемого в следующем параграфе.

Вопросы к §§ 39-42

1. Что называется контуром тела по отношению к плоскости проекций?
2. Чем задается призматическая поверхность?
3. Какие признаки позволяют установить, что на данном чертеже изображена призма (или параллелепипед)?
4. Чем задается поверхность пирамиды?
5. Что понимается под названием «тетраэдр»?
6. При каком условии для изображения пирамиды достаточно двух проекций?
7. Что называется призматоидом?
8. Что называется видом на машиностроительных чертежах?
9. В чем различие между видом и проекцией и при каком условии это различие упраздняется?
10. Какие применяются системы расположения изображений на технических чертежах?
11. Как строится фигура, получаемая при пересечении призмы или пирамиды плоскостью?
12. Как строятся точки пересечения призмы или пирамиды прямой линией (точки входа и выхода)?
13. Можно ли установить общность способов этого построения и построения точки пересечения плоскости прямой линией?
14. Как рассекается призма плоскостью, параллельной боковым ребрам призмы?
15. Как рассекается пирамида плоскостью, проходящей через вершину пирамиды?
16. Как можно применить косоугольное проецирование для нахождения точек пересечения призмы прямой линией?