Пересечение одной многогранной поверхности другою
ТеорияПостроение линии взаимного пересечения многогранных поверхностей можно производить двумя способами, комбинируя их между собой или выбирая из них тот, который в зависимости от условий задания дает более простые построения. Эти способы следующие:
1)Определяют точки, в которых ребра одной из поверхностей пересекают грани другой и ребра второй пересекают грани первой 1). Через найденные точки в определенной последовательности проводят ломаную линию, представляющую собой линию пересечения данных поверхностей. При этом можно соединять прямыми проекции лишь тех точек, полученных в процессе построения, которые лежат в одной и той же грани.
2)Определяют отрезки прямых, по которым грани одной поверхности пересекают грани другой 2); эти отрезки являются звеньями ломаной линии, получаемой при пересечении многогранных поверхностей между собой.
1) Задача на пересечение прямой линии с плоскостью.
2) Задача на пересечение двух плоскостей между собой.
Если проекция ребра одной из поверхностей не пересекает проекции грани другой хотя бы на одной из проекций, то данное ребро не пересекает этой, грани. Однако пересечение проекций ребра и грани еще не означает, что эти ребро и грань пересекаются в пространстве.
В некоторых из приводимых ниже примеров применены изложенные выше общие схемы построения точек пересечения, в других — использованы частные особенности для упрощения построений.
Пример, приведенный на рис. 268, можно рассматривать как случай пересечения пирамиды призмой. Точки 2 и 3 получаются при пересечении верхней и нижней граней призмы ребром пирамиды, а прямые, проходящие через точки 5 и 6, получаются как результат пересечения тех же граней призмы с гранью SAC пирамиды.
На рис. 280 показано пересечение поверхности треугольной призмы треугольной пирамидой; пирамида вставлена в соответствующее по форме отверстие в призме.
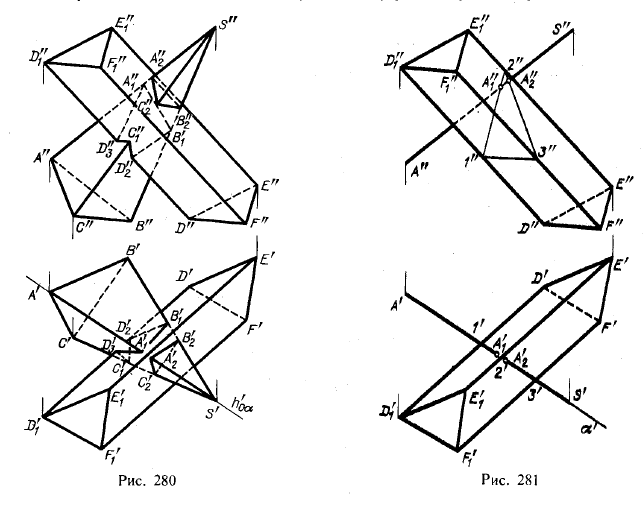
Построение основано на нахождении точек пересечения ребер одного многогранника с гранями другого. На рис. 281 показано построение точек А1 и А2, в которых ребро пирамиды SA пересекает грани в DEE1D1 и грань EFF1E1 призмы. Через ребро SA проведена пл. α (горизонтально-проецирующая), которая в горизонтальной проекции пересекает ребра призмы в точках 1', 2', 3'; по этим проекциям найдены фронтальные проекции точек пересечения пл. α с ребрами призмы 1", 2", 3". Далее отмечены точки А'[ и А"г, в которых A ".S'" пересекается с контуром 1"2"3". Точки А"1 и А"2 — фронтальные проекции точек встречи ребра SA с гранями призмы; горизонтальные проекции этих точек — точки А'1 и А'2 — находятся на горизонтальной проекции ребра SA. Поступая таким же образом с ребрами SB и SC, находим точки В1, В2, С1, С2 (рис. 280).
Затем находим пересечение ребер призмы с гранями пирамиды, также проводя вспомогательные горизонтально-проецирующие плоскости (можно, конечно, в этом случае, как и в предыдущем, воспользоваться фронтально-проецирующими плоскостями). Исследуя ребро DD1 отмечаем точки встречи D2 и D3. Ребро EE1, с гранями пирамиды не пересекаются, так же как и ребро FF1.
Для того чтобы не сделать ошибки при большом количестве вспомогательных построений, можно записывать найденные точки'встречи так:
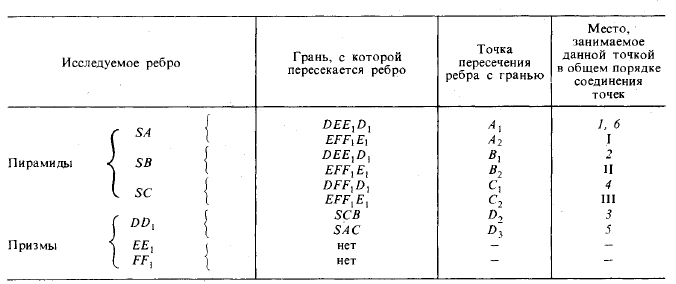
В данном примере получается два отдельных многоугольника. В таблице порядок обра зования многоугольников показан для одного цифрами 1,2 и т. д., для другого — I,II и т. д. Это означает, что точку А"1(1) следует соединить с точкой B"1(2), точку В"1 — с точкой D"2(3), D"2 - с C"1(4), C"1 - с D"3(5) и, наконец, D"3 - с А"1(6).
В построениях, показанных на рис. 280, 281, были использованы вспомогательные горизонтально-проецирующие плоскости. И хотя применение именно горизонтально- или фронтально-проецирующих плоскостей в качестве вспомогательных при нахождении точки пересечения прямой линии с плоскортью или двух плоскостей между собой (а значит, и в случаях взаимного пересечения многогранных поверхностей) удобно и является обычным приемом, могут быть случаи, когда плоскости общего положения в качестве вспомогательных окажутся предпочтительными; они дадут меньше дополнительных построений. Но для этого должны быть соответствующие условия. Пример дан на рис. 282. Здесь основания обеих пи-
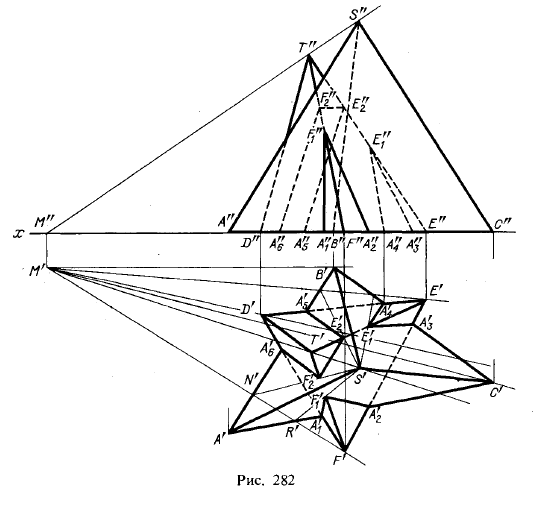
рамид находятся в одной плоскости. Через вершины пирамид проведена прямая, и найден ее след (точка М) на плоскости оснований пирамид. Всякая плоскость, проведенная через прямую ST, проходит через вершины обеих пирамид и рассекает их грани по прямым линиям (см. рис. 276); следы этих плоскостей на плоскости оснований пирамид проходят через точку М'.
Проведя, например, прямую M'F', можно принять ее за след одной из таких плоскостей; на рис. 282 след этой плоскости совпадает с проекцией M'F'.
Такая плоскость пересекает основание пирамиды ABCS в точках N' и R'; соединяя эти точки с точкой S', мы получим контур сечения пирамиды взятой плоскостью (в которой лежит ребро TF) и найдем проекции точек пересечения ребра TF — точки F'1 и F'2 нахождение фронтальных проекций этих точек пересечения не представит затруднений.
Исследуя таким приемом все ребра обеих пирамид, мы обнаружим точки, необходимые для построения линии пересечения.
Точки пересечения сторон основания определяются на горизонтальной проекции без дополнительных построений.
В нижеследующей таблице дана сводка построений.
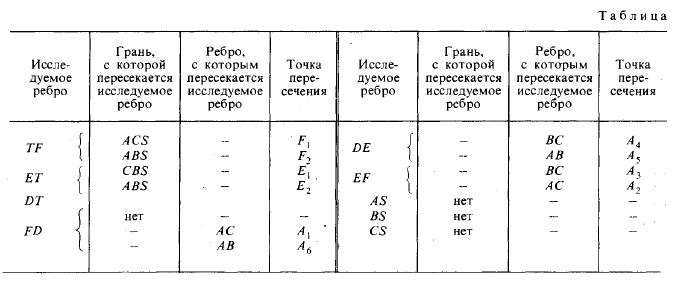
Применять указанное на рис. 282 построение можно и если основание одной из пирамид находится, например, в пл. π1, а другой — в пл. π2, При этом в общем случае надо найти следы прямой, проводимой через вершины пирамид, на пл. π1 и на пл. π2 и соответственно горизонтальный и фронтальный следы каждой вспомогательной плоскости.
Если взаимно пересекаются призма и пирамида, то'прием, показанный на рис. 282 для двух пирамид может быть применен, если провести прямую через вершину пирамиды параллельно ребрам призмы; плоскости, проводимые через такую прямую, будут рассекать грани призмы по прямым, параллельным ее ребрам, а грани пирамиды — по прямым, проходящим через ее вершину. Если же взаимно пересекаются призмы, то можно брать вспомогательные секущие плоскости параллельно ребрам обеих призм.
Возможно и применение способа перемены плоскостей проекций, если в пересечении участвует призма: получив, проекции многогранников на плоскости, перпендикулярной к ребрам призмы, используем грани призмы в этом положении в качестве секущих плоскостей.