Поверхности вращения
ТеорияВ числе кривых поверхностей — линейчатых и нелинейчатых — имеются широко распространенные в практике поверхности вращения. Поверхностью вращения называют поверхность, получаемую от вращения какой-либо образующей линии вокруг неподвижной прямой — оси поверхности 1).
Поверхность вращения можно задать образующей и положением оси. На рис. 330 показана такая поверхность. Здесь образующей служит кривая ABC, осью — прямая OO1, расположенная в одной плоскости с ABC. Каждая точка образующей описывает окружность. Таким образом, плоскость, перпендикулярная к оси поверхности вращения, пересекает эту поверхность по окружности. Такие окружно
1) В процессе образования поверхности вращения ось неподвижна.
сти называются параллелями. Наибольшую из параллелей называют экватором, наименьшую — горлом поверхности 1).
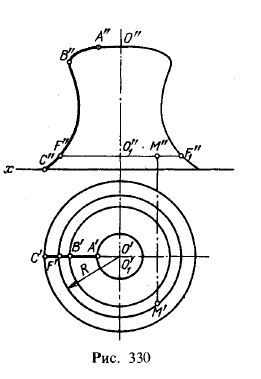
Плоскость, проходящую через ось поверхности вращения, называют меридиональной плоскостью. Линия пересечения поверхности вращения меридиональной плоскостью называется меридианом поверхности.
Можно назвать вершиной поверхности вращения точку пересечения меридиана этой поверхности с ее осью, если в пересечении не образуется прямой угол.
Если ось поверхности вращения параллельна пл. π2, то меридиан, лежащий в плоскости, параллельной пл. π2, называется главным меридианом. При таком положении главный меридиан проецируется на пл. тс2 без искажения. Если ось поверхности вращения перпендикулярна к пл. π1 то горизонтальная проекция поверхности имеет очерк в виде окружности. Наиболее целесообразным с точки зрения изображений является перпендикулярность оси поверхности вращения к пл. π1 или к π2, или к π3.
Некоторые поверхности вращения представляют собой частные случаи поверхностей, рассмотренных в § 50. Таковы: 1) цилиндр вращения, 2) конус вращения, 3) гиперболоид вращения однополостный, 4) эллипсоид вращения, 5) параболоид вращения, 6) гиперболоид вращения двуполостный.
Для цилиндра и конуса вращения меридианы являются прямыми линиями — в первом случае параллельными оси и равноудаленными от нее, во втором случае пересекающими ось в одной и той же ее точке под одним и тем же углом к оси. Так как цилиндр и конус вращения — поверхности, бесконечно простирающиеся в направлении их образующих, то на изображениях обычно их ограничивают какими-либо линиями, например следами этих поверхностей на плоскостях проекций или какой-либо из параллелей. Известные из стереометрии прямой круговой цилиндр и прямой круговой конус ограничены поверхностью вращения и плоскостями, перпендикулярными к ее оси. Меридианы такого цилиндра — прямоугольники, а конуса — треугольники.
Для гиперболоида вращения меридианом является гипербола, причем, если осью вращения служит действительная ось гиперболы, то образуется двуполостный гиперболоид вращения; если же вращать гиперболу вокруг ее мнимой оси, то однополостный.
Однополостный гиперболоид вращения может быть образован также вращением прямой линии в случае, если образующая и ось вращения — скрещивающиеся прямые.
На рис. 331 показан однополостный гиперболоид вращения, образованный вращением прямой АВ вокруг указанной оси и ограниченный двумя параллелями; окружность, проведенная из центра 01 есть горло поверхности.
На однополостном гиперболоиде вращения можно нанести прямолинейные образующие в двух направлениях, например так, как показано на рис. 331, и с наклоном в обратную сторону, под тем же углом к оси.
Кроме прямых (пар) на этой поверхности могут быть еще гиперболы, параболы, эллипсы и окружности.
1) Точнее, экватором называют ту из параллелей, которая больше соседних с нею параллелей по обе стороны от нее, рассматриваемых до первого горла; горло — наименьшая из соседних параллелей до первого экватора. Отсюда поверхность вращения может иметь несколько экваторов и горл.
На рис. 331 справа показано построение фронтальной проекции однополостного гиперболоида вращения по его оси и образующей. Прежде всего найден радиус горла поверхности. Для этого проведен перпендикуляр О'11' к горизонтальной проекции образующей. Этим определена горизонтальная проекция общего перпендикуляра к оси и образующей. Натуральная величина отрезка, выраженного проекциями O"11" и О'11', равна радиусу горла поверхности. Далее, путем поворота точки c проекциями 2",2';3",3';A",A' выведены в плоскость α,параллельную пл. π2, что
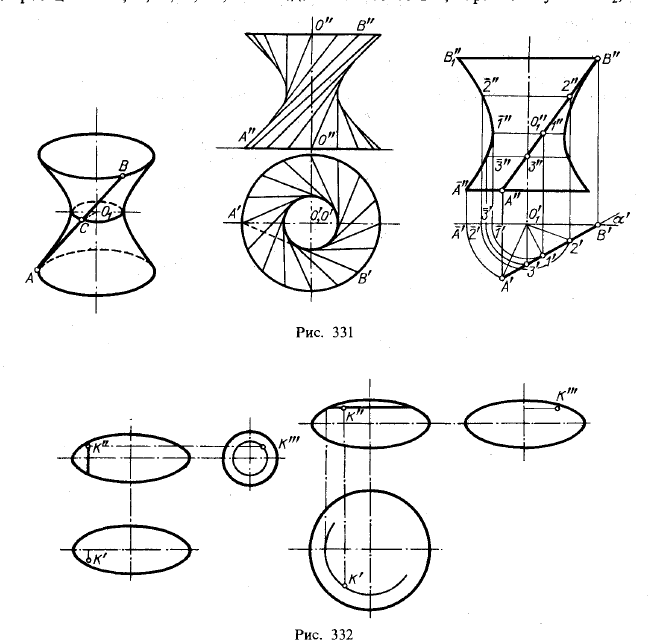
дает возможность провести очерковую линию фронтальной проекции гиперболоида. Горизонтальная его проекция представит собой три концентрические окружности.
Для параболоида вращения меридианом является парабола, ось которой служит осью поверхности.
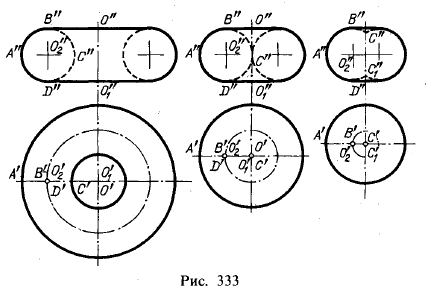
Для эллипсоида вращения меридианом является эллипс. Поверхность может быть образована вращением эллипса вокруг его большой оси («вытянутый» эллипсоид вращения — рис. 332, слева) или вокруг его малой оси («сжатый» эллипсоид вращения — рис, 332, справа). Эллипсоид вращения — поверхность ограниченная; она может быть изображена полностью. Также полностью может быть изображена и сфера. Для сферы экватор и меридианы — равные между собой окружности.
Обратим еще раз внимание на то, что такие поверхности вращения, как цилиндр, конус и однополостный гиперболоид, являются линейчатыми, т. е. их можно
образовать вращением прямой линии 1). Но эллипсоид, параболоид и двуполостный гиперболоид образуются при вращении не прямой, а эллипса, параболы и гиперболы, причем ось вращения выбирается так, чтобы образующая кривая располагалась симметрично по отношению к этой оси. То же можно сказать и относительно однополостного гиперболоида вращения, если он образуется в результате вращения гиперболы вокруг ее мнимой оси.
Так как ось вращения выбирается совпадающей с осью симметрии эллипса, параболы, гиперболы, то эллипс и Гипербола образуют по две поверхности, так как у них по две оси симметрии, а парабола — одну поверхность, так как у нее одна ось симметрии, Следовательно, каждая из образуемых поверхностей получается только при вращении одним способом. Между тем сфера, которую можно рассматривать как эллипсоид при равных большой и малой осях образующего эллипса, переходящего при этом в окружность, может быть образована вращением более чем одним
способом: образующая окружность симметрична относительно каждого из ее диаметров.
При вращении окружности (или ее дуги) вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр, получается поверхность с названием тор 2). Так называют и тело, ограниченное тором — поверхностью.
Различают (рис. 333):
1) открытый тор, иначе круговое кольцо,
2) замкнутый,
3) самопересекающийся.
На рис. 333 они изображены в простейшем положении: ось тора перпендикулярна к плоскости проекций, в данном случае к пл. π1.
Образующей для открытого и замкнутого торов служит окружность, для самопересекающегося — дуга окружности. В открытый и замкнутый торы могут быть вписаны сферы. Тор можно рассматривать как поверхность, огибающую одинаковые сферы, центры которых находятся на окружности.
Тор имеет две системы круговых сечений: в плоскостях, перпендикулярных к его оси, и в плоскостях, проходящих через ось тора 3).
1) Закономерность в расположении прямолинейных образующих однополостного гиперболоида вращения применена в конструкции, известной под названием «башня Шухова». В. Г. Шухов (1853 — 1939) — один из выдающихся русских инженеров. «Башня Шухова» применяется в устройстве радиомачт, водонапорных башен и др.
2) Фр. tore (от torus (лат.) — выпуклость, узел) — кольцеобразный выступ на колонне.
3) Существует третья система круговых сечений открытого тора, которая в книге не рассматривается.
Поверхность, называемая тором, весьма часто встречается в машиностроении и архитектуре. На рис. 334 слева изображена деталь, поверхность вращения которой содержит самопересекающийся тор и открытый тор, а справа на том же рисунке показана схематически
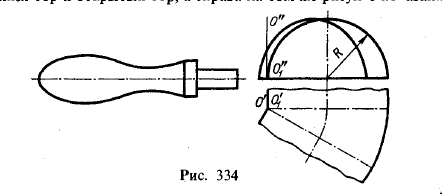
поверхность перехода от одного цилиндрического свода к другому, имеющая форму замкнутого тора с осью ОО1
Из поверхностей вращения упомянем еще катеноид 1). Эта поверхность образуется при полном обороте цепной линии 2) вокруг лежащей с ней в одной плоскости горизонтальной оси.
Положение точки на поверхности вращения определяется при помощи окружности, проходящей через эту точку на поверхности вращения.
Но это не исключает возможности применять прямолинейные образующие в случае линейчатых поверхностей вращения, подобно тому, как это показано на рис. 314 для цилиндров и конусов общего вида.
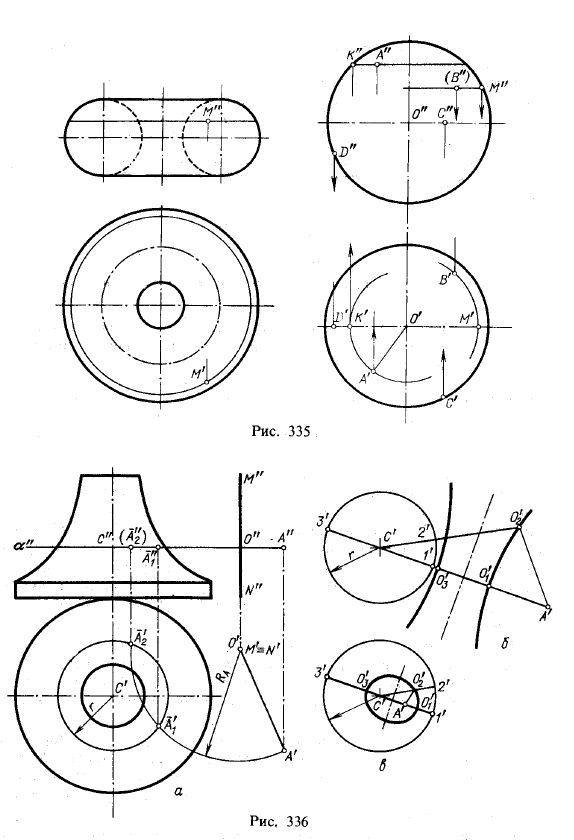
На рис. 330 показано применение параллели для построения проекции точки, принадлежащей данной поверхности вращения. Если дана проекция М", то проводим фронтальную проекцию F"F'1 параллели, а затем радиусом R = O"1F" проводим окружность — горизонтальную проекцию параллели — и на ней находим проекцию М'. Если бы была задана проекция М', то следовало бы провести радиусом R = O"1F" окружность, по точке F' найти F" и провести F"F'1— фронтальную проекцию параллели, на которой должна быть проекция М". На рис, 332 показано построение проекций точки К, принадлежащей эллипсоиду вращения, а на рис. 335 — точки М, принадлежащей поверхности кругового кольца.
На рис. 335 справа показано нахождение проекций точек на сфере. По данной проекции А' точки А построена фронтальная проекция А"; по данной проекции В" найдена горизонтальная проекция В' точки В, удовлетворяющей дополнительному условию, что точка В невидима, если смотреть на пл. π2.
Точка С задана на экваторе: ее проекция С' находится на очерке горизонтальной проекции сферы, т. е. на горизонтальной проекции экватора. Точки К и М лежат на главном меридиане; они принадлежат параллелям, на которых находятся точки А и В. Точка D также находится на главном меридиане, причем она невидима, если смотреть на пл. π1.
Рассмотрим пример построения проекций точек, принадлежащих поверхности вращения. Пусть требуется привести точку А, вращая ее вокруг данной оси MN, на заданную поверхность вращения (рис. 336, а). Так как в данном случае ось поверхности вращения и ось вращения точки А перпендикулярны к плоскости проекций π1, то окружность вращения точки А проецируется на π1 без искажения, равно как и та параллель поверхности вращения, которая получается при пересечении этой поверхности плоскостью вращения точки А. В этой плоскости расположен и центр вращения точки А — точка О (точка пересечения оси вращения MN с плоскостью вращения α). Остальное ясно из чертежа. В положении А2 на поверхности точка окажется невидимой на пл. π2.
2) Catena (лат.) — цепь.
2) Цепная линия — кривая, форму которой принимает цепь, подвешенная в ее двух точках, или вообще тяжелая нерастяжимая нить, подвешенная за ее концы.
Положим, что будет поставлен вопрос о выборе оси вращения для того, чтобы далее точка А могла оказаться на заданной поверхности вращения, На с. 100 был рассмотрен аналогичный вопрос, но там требовалось выбрать ось, чтобы поворотом вокруг нее можно было ввести точку в плоскость, Тогда было установлено, что имеется зона, в которой нельзя брать оси, так как при повороте вокруг таких осей точка не соприкоснется с плоскостью. Эта зона определялась параболическим цилиндром, причем парабола возникла при рассмотрении взаимного положения вращаемой точки и прямой, на которой эта точка должна была бы оказаться, соприкоснувшись с плоскостью.
Теперь, очевидно, вопрос будет, решаться при рассмотрении взаимного положения точки А и окружности (параллели) на поверхности тела вращения,
Из рис. 336, а следует, что проекция О' центра вращения должна быть расположена так, чтобы RA не был меньше расстояния точки О' до ближайшей точки на проекции окружности радиуса r, Если же взять точку О' на равных расстояниях от А' и от проекции этой окружно
сти (например, в О'1 или O'2; см. рис, 336,6), то в ней уже можно установить ось вращения; окружность вращения точки А коснется окружности радиуса r, т, е, точка А соприкоснется с поверхностью вращения.
Где на чертеже лежат все точки, одинаково удаленные от точки А' и от окружности радиуса r? Они расположены на гиперболе (рис, 336,6), для которой точка А' служит одним из фокусов, точка О'1, в которой отрезок А'1' делится пополам, — одной из вершин. Если разделить отрезок А'З' пополам, то мы получим вторую вершину гиперболы (точка О'3); второй фокус расположится в точке С', т. е. в центре окружности, полученной при пересечении поверхности тела вращения плоскостью α (рис. 336, а).
Из рассмотренного вытекает, что точки, расположенные на обеих ветвях гиперболы или между ними, могут быть выбраны каждая в качестве горизонтальной проекции оси вращения.
Может быть случай, когда точка находится внутри поверхности вращения. Следовательно, проводя через точку плоскость вращения, мы получим проекцию А' внутри проекции окружности радиуса r, по которой плоскость вращения точки А пересекает поверхность вращения (рис, 336, в). И на этот раз очевидно, что RA не должен быть меньше расстояния точки О' (т, е, проекции оси) до ближайшей точки проекции окружности радиуса r. Предельные положения проекций осей расположатся теперь как точки эллипса с фокусами в точках А' и С', с большой осью на прямой 1'З', с вершинами в точках O'3 и O'3. Внутри этого эллипса не следует брать проекции осей; такие оси не дадут возможности ввести точку А в поверхность вращения,
Итак, вопрос, как выбрать ось вращения, чтобы, вращая вокруг нее точку, ввести эту точку в плоскость или в поверхность вращения, ось которой параллельна оси вращения, привел нас к эллипсу (рис. 336, в), -параболе (рис, 244), гиперболе (рис. 336,6) как геометрическим местам центров вращения.
При решении различных задач применяются те или иные поверхности в качестве геометрических мест точек или линий, отвечающих определенным условиям. Например, заданы пл. α и точка К вне этой плоскости; определить, как расположатся в пл. α точки, отстоящие от точки К на заданное расстояние r (расстояние r больше, чем расстояние точки К до пл. α). В данном случае решение связано с применением сферы как геометрического места точек, отстоящих от точки К на расстояние r, Плоскость α пересечет эту сферу по окружности, которая,и даст решение задачи .
Если бы требовалось построить в пл. α точки, отстоящие на расстояние r не от точки, а от некоторой прямой АВ, не лежащей в пл. α, то геометрическим местом таких точек в пространстве оказалась бы поверхность цилиндра вращения с осью АВ и радиусом r, а искомые в пл. α точки получились бы на линии пересечения этого цилиндра пл. α.
В дальнейшем на рис. 368 справа и 401 можно видеть примеры применения конических поверхностей вращения как геометрических мест прямых, проходящих через заданную точку.
Если в задаче поставлен вопрос о точках, равноотстоящих от заданных плоскости α и точки М, то в качестве геометрического места таких точек в пространстве следовало бы использовать параболоид вращения с фокусом параболы в точке М.
Применение тех или иных поверхностей в качестве геометрических мест, конечно, не исчерпывается приведенными примерами.
Вопросы к § 51
- Что называется поверхностью вращения?
- Чем можно задать поверхность вращения?
- Что называется параллелями и меридианами на поверхностях вращения, экватором, горлом, главным меридианом?
- Какая из осей гиперболы служит осью вращения для образования: а) однополостного, б) двуполостного гиперболоида вращения?
- Можно ли образовать однополостный гиперболоид вращения при помощи прямой линии?
- Какие поверхности вращения (кроме однополостного гиперболоида) являются линейчатыми?
- Как образуется поверхность, называемая тором?
- В каком случае для тора применяется название «круговое кольцо»?
- Сколько систем круговых сечений имеет тор?
- Как определяется положение точки на поверхности вращения?
1) Предлагаем читателю составить чертеж и выполнить решение этой и последующих задач.