Развертка поверхности многогранников
ТеорияРазвертка поверхности многогранников известна читателю из средней школы. Поэтому на этом вопросе мы останавливаемся кратко, только в плане повторения известных ранее сведений.
Под разверткой многогранной поверхности подразумевают плоскую фигуру, составленную из граней этой поверхности, совмещенных с одной плоскостью.
Существуют три способа построения развертки многогранных поверхностей:
1) способ нормального сечения;
* Геометрическое преобразование, при котором сохраняются величины углов, называется конфорным, следовательно, построение разверток является конфорным преобразованием, а поверхность и ее развертка конфорны.
** Геодезической называется линия, принадлежащая поверхности и соединяющая кратчайшим путем две точки, также принадлежащие поверхности.
2) способ раскатки;
3) способ треугольников (триангуляции).
Первые два применяются для построения развертки призматических поверхностей, третий - для пирамидальных поверхностей. Рассмотрим каждый их этих способов.
1. Способ нормального сечения.
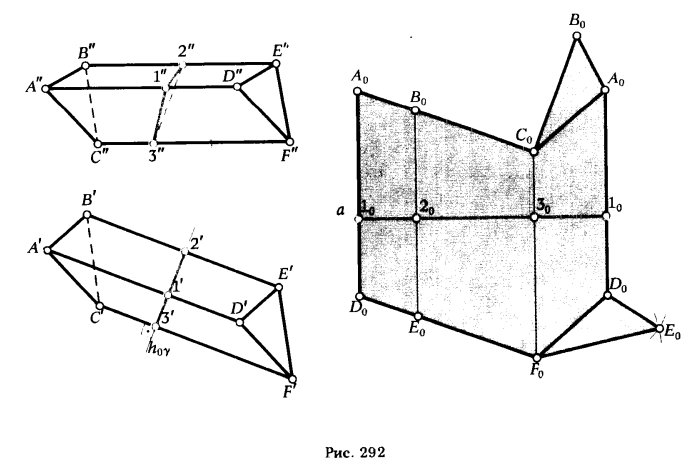
ПРИМЕР. Построить развертку наклонной трехгранной призмы ABCDEF (рис. 292).
РЕШЕНИЕ. Пересечем призму ABCDEF плоскостью γ, перпендикулярной к боковым ребрам призмы. Построим сечение заданной призмы этой плоскостью — Δ123. Определим длины сторон Δ123. В свободном месте чертежа проведем прямую а (на рис. 292 прямая а проведена горизонтально). От произвольной точки 10, взятой на этой прямой, отложим отрезки [1020], [ 2030], [3010], конгруентные сторонам Δ123. Через точки 10, 20, 30, 10 проведем прямые,
перпендикулярные к прямой а , и отложим на них от точек 10, 20, 30, 100 отрезки, конгруентные соответствующим длинам боковых ребер ([1А], [ ID], [2В], [ 2Е], ...). Полученные точки А0В0C0A0 и D0 Е0 F0 D0 соединяем прямыми. * Плоская фигура A0B0C0A0D0F0E0D0 представляет собой развертку боковой поверхности призмы.
Чтобы получить полную развертку призмы, необходимо к развертке боковой поверхности пристроить основания призмы — ΔА0В0С0 и ΔD0E0F0, предварительно определив их неискаженные размеры.
* На рис. 292 ребра АD ВЕ и CF параллельны плоскости π1, поэтому они проецируются ца эту плоскость без искажения. Если ребра призмы занимают произвольное положение, то прежде чем приступить к построению развертки, следует с помощью способов преобразования перевести их в положение, параллельное какой-либо плоскости проекции.
2. Способ раскатки.
Этот способ целесообразно использовать для построения развертки поверхности призмы в том случае, когда основание призмы параллельно какой-либо одной плоскости проекции, а ее ребра параллельны другой плоскости проекции.
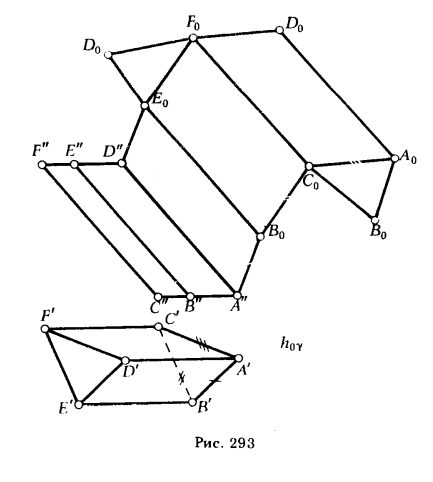
ПРИМЕР. Построить развертку боковой поверхности наклонной трехгранной призмы ABCDEF (рис. 293).
РЕШЕНИЕ. Примем за плоскость развертки плоскость γ, проходящую через ребро AD, параллельную фронтальной плоскости проекции. Совместим грань ADEB с плоскостью γ. Для этого мысленно разрежем боковую поверхность призмы по ребру AD, а затем осуществим поворот грани ADEB вокруг ребра AD (A"D").
Для нахождения совмещенного с плоскостью γ положения ребра В0Е0 из точки В" проводим луч, перпендикулярный к A"D" и засекаем на нем дугой радиуса |А'В'| , проведенной из центра А", точку B0. Через B0 проводим прямую В0Е0, параллельную (A"D").
Принимаем совмещенное положение ребра B0E0 за новую ось вращения и поворачиваем вокруг нее грань BEFC до совмещения с плоскостью γ. Для этого из точки С" проводим луч, перпендикулярный к совмещенному ребру B0E0, а из точки В0 — дугу окружности радиусом, равным |В'С'|; пересечение дуги с лучом определит положение точки С0. Через С0 проводим С0F0 параллельно В0Е0. Аналогично находим положение ребра А0D0. Соединив точки А"В0C0A0 и D"E0F0D0 прямыми, получим фигуру A"B0C0A0D0F0E0D" — развертку боковой поверхности призмы. Для получения полной развертки призмы достаточно к какому-либо из звеньев ломаной линии А"В0С0А0 и D"E0F0D0 пристроить треугольники основания А0В0С0 и D0E0F0.
3. Способ треугольников (триангуляции).
ПРИМЕР. Построить развертку боковой поверхности пирамиды SABC (рис. 294).
Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников — граней пирамиды.
На рис. 294 определение длин ребер пирамиды выполнено с помощью вращения их вокруг оси i ∋ S и i ⊥ π1. Путем вращения ребра пирамиды совмещаются с плоскостью γ плоскость γ || π2 и γ ⊃ i . После того как определены длины ребер |S"A2|, |S"B2|, |S"C2|, приступаем к пост-
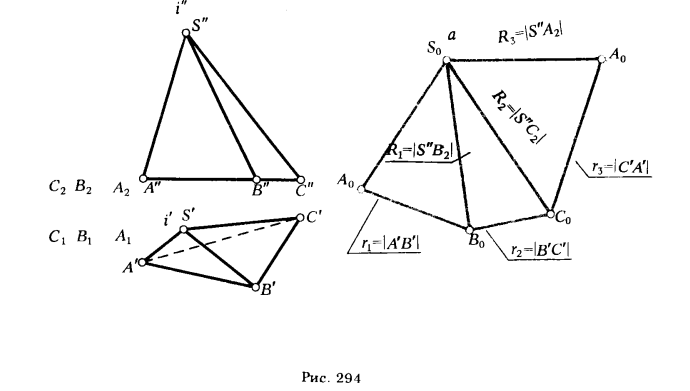
роению развертки. Для этого через произвольную точку S0 проводим прямую а. Откладываем на ней от точки S0[S0А0] ≅ [S"A2]. Из точки A0 проводим дугу радиусом r1 = |А'В'|, а из точки S0 — дугу радиусом R1 = |S"B2|. Пересечение
дуг укажет положение вершины В0 ΔS0A0B0 ( ΔS0A0B0 ≅ ΔSAB — грани пирамиды). Аналогично находятся точки С0 и A0. Соединив точки A0В0С0A0, получим развертку боковой поверхности пирамиды SABC.