Некоторые косоугольные аксонометрические проекции

Из числа косоугольных аксонометрических проекций остановимся прежде всего на часто применяемой проекции, получаемой на плоскости, параллельной пл. π₂. Если плоскость аксонометрических проекций α параллельна пл. π₂, то не следует направление проецирования выбирать параллельно пл. π₃, так как проекции координатных осей займут положение, при котором аксонометрическое изображение получается мало наглядным. Направление проецирования следует выбрать так, чтобы проекции координатных осей на пл. α располагались, как указано на рис. 480. При этом отрезки по осям х и z проецируются без искажения, равно как и самый

угол xO_αaz; таким образом, по осям O_αх и O_αz на плоскости α коэффициенты искажения ривны единице. Что же касается оси γ, то соответствующий ей коэффициент искажения может иметь различные значения, в том числе и единицу; в последнем случае мы будем иметь изометрическую косоугольную проекцию. Если же коэффициент искажения по оси О_αу не равен единице, то косоугольная аксонометрическая проекция на пл. α будет диметрической.

Отрезок ОО_α. параллельный направлению проецирования, и отрезки О_γ и O_1γ определяют прямоугольный треугольник ОуО₁ (угол 0у0₁ прямой). В самом деле, отрезок Оу перпендикулярен к пл. π₂, а так как пл. α параллельна пл. π₂, то, следовательно, пл. α перпендикулярна к Оу. Вращая треугольник ОуО₁ вокруг катета Оу, можно получить различные

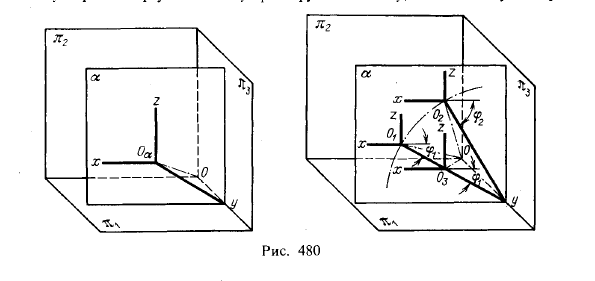
положения точки O₁ на пл. α, причем во всех своих положениях точка О₁ находится на одном и том же расстоянии от оси γ: геометрическим местом положений точки О₁ будет окружность, описанная из точки у радиусом уО₁. На рис. 480 справа указано два таких положения: O₁ и O₂; каждая из точек О₁ и O₂ служит началом осей, из которых оси х и z сохраняют свои направления, а ось y меняет направление; это выражается изменением угла φ между аксонометрическими осями х и у. При этом направление проецирования меняется (см. на рис. 480 направление отрезков OO₁ и OO₂). Угол φ можно выбрать произвольно.

С другой стороны, если взять на пл. α начало осей в точке O₃ на отрезке уO₁, т. е. взять направление проецирования параллельно направлению отрезка OO₃, то величина угла φ₁, остается неизменной, в то время как O₃y/Oy -не равно отношению- O₁y/Oy ; это отношение представляет собой коэффициент искажения по оси у. Следовательно, можно выбирать произвольно как величину коэффициента искажения по оси у, так и величину угла φ с целью получить наиболее выразительное изображение.

Рассматриваемую нами косоугольную аксонометрическую проекцию па плоскости, параллельной пл. π₂, называют «фронтальной проекцией», а также «кавальерной проекцией» или «кавальерной перспективой». Очень часто применяют тот случай фронтальной проекции, когда для коэффициента искажения по оси у выбрано значение 0,5, а угол φ взят равным 45°; такая проекция называется иногда «кабинетной проекцией» ¹).

Изображение куба в кабинетной проекции дано на рис. 481. Передняя грань повторяет проекцию на пл. π₂. Поэтому окружность, вписанная в эту грань, останется окружностью и в кабинетной проекции. Отсюда можно вывести заключение, что кабинетная проекция, представляющая собой весьма простой и наглядный способ изображения тел с прямолинейными очертаниями, удобна и для построения изображений в тех случаях, когда приходится иметь дело с окружностями, расположенными в плоскостях, параллельных аксонометрической плоскости проекций, т. е. || π₂.

¹) Cabinet projection (англ.).

Если же приходится в кабинетной проекции изображать окружность, расположенную в плоскости, параллельной пл. проекций π₁ и π₃, то эту окружность вписывают в квадрат, строят параллелограмм, являющийся кабинетной проекцией этого квадрата, затем намечают на окружности ряд точек и строят их проекции. Они будут расположены на эллипсе — проекции окружности.

На рис. 482 показано построение точек эллипса — проекции окружности, расположенной в плоскости, параллельной пл. π₁. Прежде всего, окружность вписывается

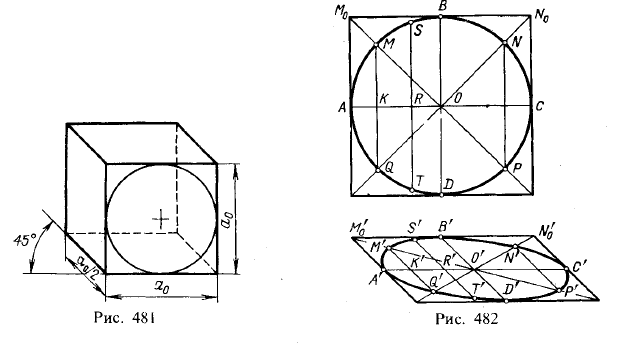
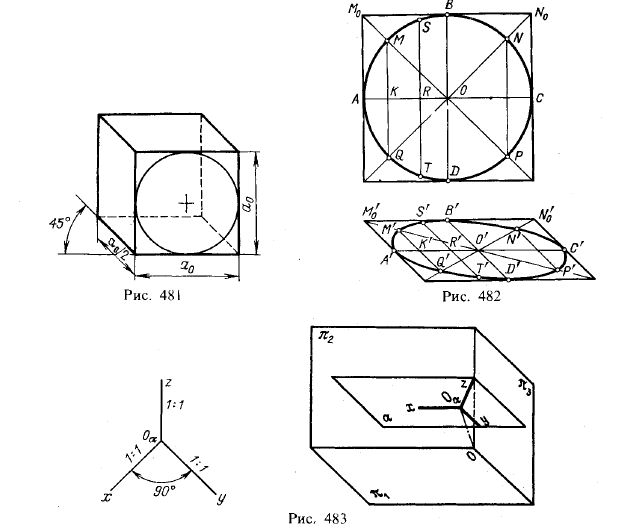
в квадрат и строится проекция этого квадрата. Диаметр АС сохраняет свою длину и направление (получаем точки А' и С'; диаметр BD, перпендикулярный к АС, займет положение под углом 45° к А'С' и сократится вдвое (точки В' и D'). Хорды MQ и NP, получаемые при проведении диагонали квадрата, дают еще четыре точки (М', Q', N', Р'), причем

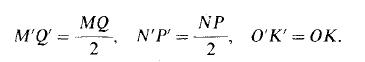
Далее, взят произвольный отрезок OR и отложен по направлению О'А'; через точку R' проведен отрезок S'T', параллельный B'D' и равный ST:2. Получаются еще две точки (S' и Т'), лежащие на искомом эллипсе. Поступая аналогично, можно найти ряд точек, через которые проходит эллипс.

Построение проекции окружности, расположенной в плоскости, параллельной π₃, аналогично рассмотренному.

Отметим также случай косоугольной аксонометрической проекции, когда плоскость аксонометрических проекций параллельна пл. π₁ (рис. 483). При таком расположении плоскости α угол хО_αу = 90°. Что же касается оси z, получаемой на пл. α, то соответствующий ей коэффициент искажения выражается отношением O_αz: Oz (отрезки 0_αz и Oz представляют Собой катеты прямоугольного треугольника OzO_α прямой угол — в точке z). В тех случаях, когда

применяют такую косоугольную аксонометрическую проекцию, направление проецирования берут под углом 45° к пл. α (или к пл. π₁). При этом отрезок O_αz равен отрезку Oz, т. е. коэффициент искажения по оси z получается равным единице и сама проекция получается изометрической.

Вопросы к главе XII

1. В чем заключается способ аксонометрического проецирования?
2. Что называется коэффициентами (или показателями) искажения?
3. Что называется вторичной проекцией точки?
4. Как производится переход от прямоугольных координат к аксонометрическим?
5. В чем заключается «основное предложение аксонометрии» (иначе «основная теорема аксонометрии»)?
6. В каких случаях аксонометрическая проекция называется: а) изометрической, б) диметрической, в) триметрической?
7. В чем различие между косоугольной и прямоугольной аксонометрическими проекциями?
8. Какая линия является очерком аксонометрической проекции сферы: а) косоугольной, б) прямоугольной?
9. Чему равняется сумма квадратов коэффициентов искажения для прямоугольной аксонометрической проекции?
10. Чему равняются коэффициенты искажения в прямоугольной проекции: а) изометрической, б) диметрической (при соотношении коэффициентов 1:0,5: 1) — и каковы эти коэффициенты в приведенном (к единице) виде?
11. Что такое «треугольник следов» и какие выводы из него можно сделать в прямоугольных аксонометрических проекциях?
12. Как строятся оси в прямоугольных проекциях: а) изометрической, б) диметрической (1:0,5:1)?
13. Как определяется направление и величина малой оси эллипса, являющегося изометрической или диметрической проекцией окружности, расположенной в а) плоскости общего положения, б) плоскостях фронтально-проецирующей и горизонтально-проецирующей, в) плоскостях фронтальной, горизонтальной и профильной?
14. В каких случаях прямоугольная аксонометрическая проекция окружности может оказаться отрезком прямой линии или окружностью?
15. Как определить координаты точек, заданных в прямоугольной аксонометрической проекции на поверхности: а) сферы, б) цилиндра вращения, в) конуса вращения?
16. Какая косоугольная аксонометрическая проекция называется: а) фронтальной или кавальерной, б) кабинетной?