Стандартные аксонометрические проекции
ТеорияВ инженерной практике, в частности в машиностроении, наибольшее распространение получили прямоугольные диметрические и изометрические проекции. Отметим некоторые свойства этих проекций.
1. Зависимость коэффициентов искажения по аксонометрическим осям от направления проецирования.
Установление зависимости между коэффициентами искажения и направлением проецирования представляет определенный практический интерес.
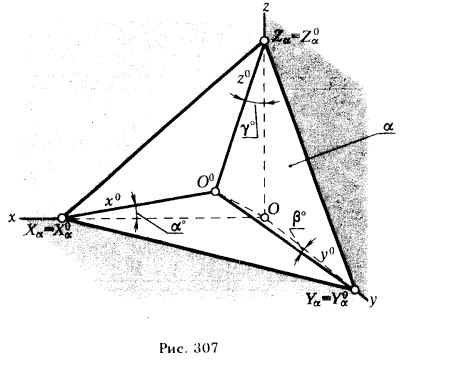
Картинная плоскость пересекает координатные оси в точках Хα ≡ Х0α, Yα ≡ Y0α, Zα ≡ Z0α, а плоскости проекций по прямым ХαYα, XαZα, YαZα. Точки Xα, Yα, Zα определяют треугольник, называемый треугольником следов (рис. 307). Очевидно, ΔXαYαZα ≡ ΔX0αY0αZ0α.
Опустим из начала координат О перпендикуляр на плоскость α. Точка О0, в которой этот перпендикуляр пересекает плоскость α, является прямоугольной проекцией точки О. Отрезки О0Х0α, О0Y0α и О0Z0α - прямоугольные аксонометрические проекции отрезков координатных осей ОХα, OYα, OZα. Треугольники ОО0Х0α, OO0Y0α, ОО0Z0α - пря 208 моугольные, отрезки O0Х0α, О0Y0α, О0Z0α - их катеты, а отрезки ОХ0α, OY0α, OZ0α - гипотенузы этих треугольников. Отсюда
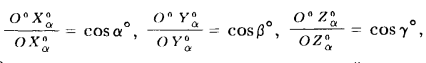
где α° , β°, γ° - углы наклона осей х, у, z к картинной плоскости.
Так как 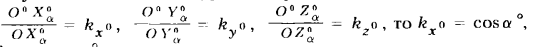
ky0 = cosβ°, kz0 = cosγ°
В прямоугольной аксонометрии коэффициенты искажения связаны зависимостью k2x0 + k2y0 + k2z0 = 2
Изометрическая проекция. В прямоугольной изометрической проекции коэффициенты искажения по всем осям одинаковы:
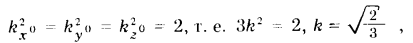
следовательно, коэффициенты искажения но осям x0, у0, y0 равны 0,82.
Изометрическую проекцию, как правило, выполняют без искажения (т. е. коэффициент искажения k = 1), что соответствует увеличению линейных размеров изображения по сравнению с действительными в 1,22 раза (1/0,82 ≈ 1,22).
Диметрическая проекция. Для прямоугольной диметрической проекции характерно равенство коэффициентов искажения по двум осям kx0 = kz0; коэффициент искажения по третьей оси ky0 = 1/2kx0 (или ky0 = 1/2kz0 ). Поэтому 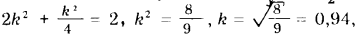 , т. е. коэффициент искажения по осям x0 и z0 равен 0,94, а по оси у0 = 0,47. Диметрическую проекцию, как и изометрию, выполняют, как правило, без искажения по осям x0 и у0 и с искажением ky0 = 0,5 по оси у0. В этом случае увеличение линейных размеров изображения по сравнению с действительными происходит в 1/0,94 = 1,06 раза.
, т. е. коэффициент искажения по осям x0 и z0 равен 0,94, а по оси у0 = 0,47. Диметрическую проекцию, как и изометрию, выполняют, как правило, без искажения по осям x0 и у0 и с искажением ky0 = 0,5 по оси у0. В этом случае увеличение линейных размеров изображения по сравнению с действительными происходит в 1/0,94 = 1,06 раза.
2. Определение углов между осями стандартных аксонометрических проекций.
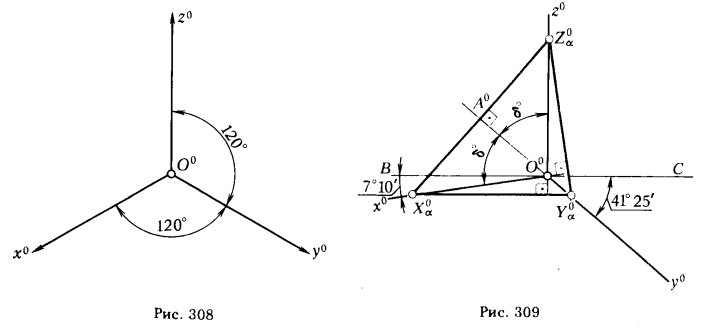
Изометрическая проекция. Для прямоугольной (ортогональной) аксонометрии справедливо следующее утверждение: коэффициенты искажения по аксонометрическим осям равны косинусам углов наклона координатных осей к картинной плоскости (доказательство см. п. 1). Так как для изометрии kx0 = ky0 = kz0 = 1, то отрезки О0X0α = О0Y0α = O0Z0α. Это, в свою очередь, означает, что в прямоугольной аксонометрии треугольник следов равносторонний.
В теории ортогональных аксонометрических проекций доказывается, что аксонометрические оси являются высотами треугольника следов. Из элементарной геометрии известно, что в равностороннем треугольнике высоты попарно пересекаются между собой под углом в 120°. Поэтому совпадающие с ними аксонометрические оси в ортогональной изометрии образуют между собой углы в 120°. Обычно ось z° принимают вертикальной (рис. 308).
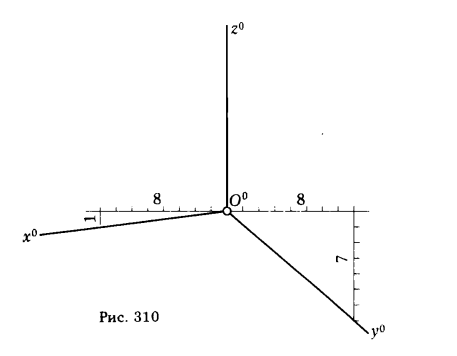
Диметрическая проекция. Для диметрической проекции характерно равенство двух коэффициентов искажения по осям х0 и z0, коэффициент искажения по третьей оси равен их половине:
kx0 = kz0 = 2ky0.
Равенство kx0 = kz0 обеспечивает конгруентность отрезков О0X0α = О0Z0α, т. е. треугольник следов - равнобедренный (рис. 309). В этом треугольнике высота Y0αA0, совпадающая с направлением аксонометрической оси y0, делит пополам сторону X0αZ0α; |Х0αА0| = |А0Z0α| = √2/2 .
Приняв |О0Х0α| = |О0Z0α| = 1, имеем X0αZ0α = √2 . Из ΔО0A0Z0α определяем sinδ°:
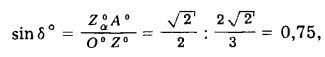
что соответствует равенству угла 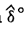 = 48°35'. Тогда
= 48°35'. Тогда
∠X0αO0Z0α = 2∠δ° = 97°10'
Обычно при построении диметрических проекций ось z° располагают вертикально. Тогда треугольник следов и его высоты (аксонометрические оси) займут положение, показанное на рис. 309. В этом случае
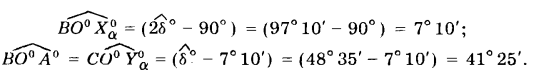
Приближенно аксонометрические оси стандартной диметрии можно построить, если принять tg7°10' ≈ 1/8, a tg41°25' = 7/8. Тогда аксонометрические оси х0 и у0 проводят так, как это показано на рис. 310. Ось у0 может быть проведена так же, как продолжение биссектрисы ∠х0О0z0 .