Примеры построения аксонометрических проекций геометрических фигур

При построении аксонометрических проекций пользоваться коэффициентами искажения неудобно. Поэтому обычно строят рекомендованные ГОСТ 2.317-69 (СТ СЭВ 1979-79) стандартные прямоугольные изометрию и диметрию, принимая соответствующие масштабы увеличения в 1,22 раза для изометрии и в 1,06 раза для диметрии. Введение этих масштабов позволяет строить аксонометрические проекции без сокращения размеров, откладываемых по аксонометрическим осям. Для диметрической проекции размеры по оси у⁰ сокращают вдвое.

А. Построение аксонометрических проекций геометрических фигур, ограниченных отрезками прямых и отсеками плоскостей.

При параллельном проецировании на плоскость прямые проецируются в прямые (см. § 6, 1а), следовательно, Для построения аксонометрического изображения прямой а достаточно определить аксонометрические проекции двух принадлежащих ей точек, которые однозначно определяют прямую а⁰ - аксонометрическую проекцию прямой а .

Построение аксонометрических проекций многогранников, в частном случае многоугольников, сводится к определению аксонометрических проекций их вершин, которые затем соединяют между собой отрезками прямых линий.

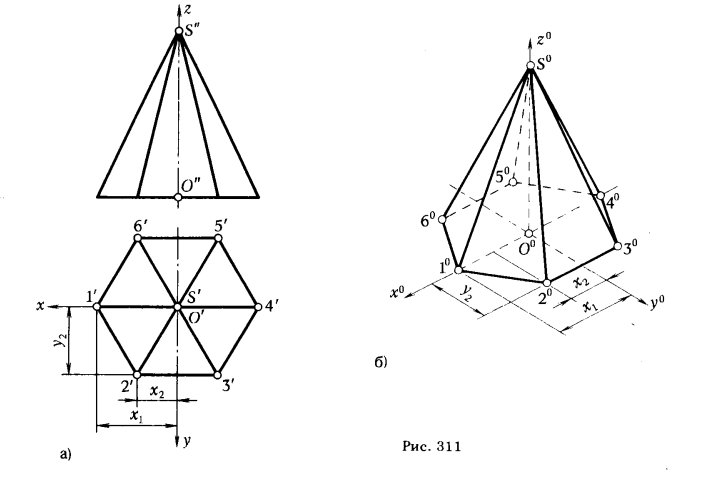
На рис. 311,6 показано построение стандартной изометрической проекции шестигранной пирамиды, ортогональные проекции которой заданы на рис. 311, а. Построение выполняем в следующей последовательности: проводим прямые х, у, z, которые принимаем за оси натуральной системы координат; за начало координат принимаем точку О (O', О"). Затем проводим аксонометрические оси х⁰, у⁰, z⁰. Измерив на ортогональном чертеже натуральные координаты вершин основания пирамиды (точки 1, 2, 3, 4, 5, 6) и ее вершины (точка S), строим их аксонометрические проекции (точки 1⁰, 2⁰, 3⁰, 4⁰, 5⁰, 6⁰, S⁰). Чтобы получить изометрическую проекцию пирамиды, соединяем полученные точки отрезками прямых линий в той же последовательности, в какой они соединены на ортогональных проекциях.

Б. Построение аксонометрических проекций геометрических фигур, ограниченных кривыми линиями и поверхностями.

В общем случае аксонометрической проекцией кривой линии (или поверхности) будет также кривая линия (поверхность).

Пример построения стандартной изометрии произвольной пространственной кривой l показан на рис. 312. Построение аксонометрических

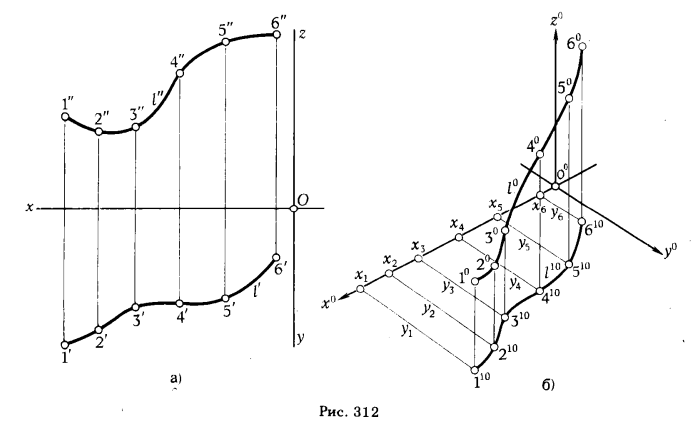
проекций точек, принадлежащих кривой l, осуществляется в последовательности, указанной ниже.

1. Относим данную линию к некоторой натуральной системе координат Oxyz.

2. Отмечаем на кривой l точки 1, 2, 3, ... и определяем их ортогональные координаты (рис. 312,а).

3. По координатам точек 1, 2, 3, ... строим их вторичные проекции 1^{1 0}, 2^{1 0}, З^{1 0}, ... (рис. 312,6).

4. Через вторичные проекции точек проводим прямые, параллельные аксонометрической оси z⁰, и откладываем на них отрезки, равные значению соответствующих аппликат точек (1, 2, 3, ...); находим точки 1⁰, 2⁰, 3⁰, ...

5. Соединив найденные аксонометрические проекции точек 1⁰, 2⁰, 3⁰, ... плавной линией, получим аксонометрическую проекцию кривой l⁰.

В практике построения аксонометрических проекций машиностроительных деталей часто приходится строить аксонометрические проекции окружностей. В большинстве случаев плоскости окружностей бывают параллельны какой-либо из координатных плоскостей. Рассмотрим возможные варианты построения окружности в изометрической и диметрической проекциях.

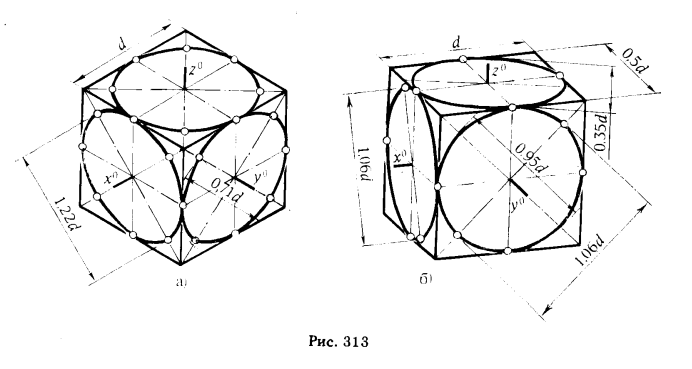
Чтобы иметь более наглядное представление о расположении и величине осей эллипсов, в которые проецируются окружности, последние вписаны в грани куба. На рис. 313,а показана проекция куба в изометрии, а на рис. 313,6 - в диметрии. Окружность, вписанная в грань куба, касается его ребер в их середине. Так как касание является инвариантом параллельного проецирования, то в аксонометрических проекциях точки касания эллипсов, в которые преобразуются окружности, будут нахо диться так же в серединах ребер куба. Кроме.этих четырех точек можно указать еще четыре точки, принадлежащие концам большого и малого диаметров эллипса. В прямоугольных изометрических и диметрических проекциях направления больших осей эллипсов перпендикулярны свободным аксонометрическим осям, а малые оси эллипсов совпадают по направлению со свободными аксонометрическими осями.

Для прямоугольной (практической) изометрии величина большого диаметра эллипса равна l,22d окружности, малого диаметра - .0,71d (см. рис. 313,а). В прямоугольной диметрии большой диаметр эллипса равен l,06d, малый диаметр для эллипсов, расположенных в гранях куба, параллельных координатным плоскостям Оху и Oyz, равен 0,35d. Для эллипса, принадлежащего греши куба, параллельной плоскости Oxz, малый диаметр решен 0,95d (см. рис. 313,6).

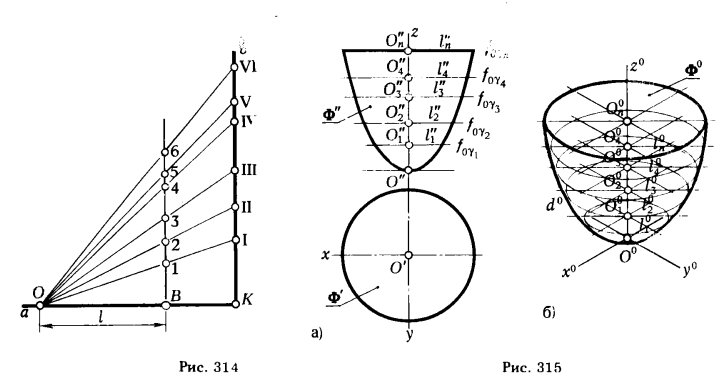
Чтобы исключить арифметические подсчеты при определении длин отрезков, умноженных на величину масштаба искажения, следует пользоваться пропорциональным масштабом. Для его построения достаточно провести две взаимно перпендикулярные прямые а и b (рис. 314) и на одной из них от точки пересечения К отложить [КО], равный 100 единицам, а на другой - отрезки [KI], [КII], [KIII], [KIV], [KV], [КVI], соответственно равные 35, 50, 71, 95, 106, 122 единицам измерения. Точки I, II, ...VI соединяем с точкой О. Если теперь от точки О на прямой ОК отложить [ОВ] заданной длины l и из конца В отрезка [ОВ] восставить перпендикуляр к [ОК], то он пересечет прямые (0I), (ОII), (ОIII), (OIV), (OV), (OVI) в точках 1, 2, 3, 4, 5, 6. Полученные отрезки [В1], [В2], [ВЗ], [В4], [В5], [В6] будут равны соответственно 0,35l, 0,5l, 0,71l, 0,95l, 1,06l, 1,22l.

Если плоскость окружности занимает произвольное положение по отношению к координатным плоскостям, то построение аксонометрической проекции окруж;ности осуществляется так же, как это делается при построении аксонометрической проекции кривой (см. с. 215 п. Б, рис. 312). Построение аксонометрических проекций поверхностей, ограничивающих геометрические фигуры, можно осуществить двумя способами:

1. Способ сечений. Этот способ заключается в следующем:

1) поверхность геометрической фигуры, аксонометрическую проекцию которой требуется построить, рассекаем плоскостями γ₁, γ₂,γ₃,..., γ_n (Рис- 315);

2) определяем линии пересечения заданной фигуры Ф плоскостями γ_j(l₁, l₂, l₃, ..., l_n);

3) строим аксонометрические проекции линий l₁, l₂, l₃, ..., l_n → l⁰₁, l⁰₂, l⁰₃, ..., l⁰_n; для упрощения определения, линий l_j и построения их аксонометрических проекций секущие плоскости следует принимать параллельными какой-либо плоскости проекции;

4) кривая d⁰, огибающая линии l⁰₁, l⁰₂, l⁰₃, ..., l⁰_n, является очерковой линией - линией видимого контура фигуры Ф⁰ .

2.Способ вписывания сферических поверхностей. Целесообразность применения этого способа основывается на том, что в прямо-

угольной аксонометрии поверхность сферы проецируется на картинную плоскость в виде круга. Этот способ следует использовать в тех случаях, когда фигура ограничена поверхностью вращения. Так как в любую поверхность вращения могут быть вписаны сферические поверхности, то аксонометрическую проекцию поверхности вращения можно рассматривать как огибающую этих сфер.

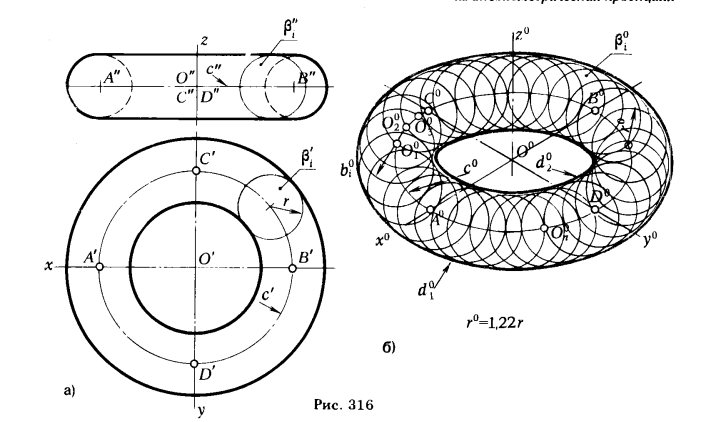
Сущность способа покажем на конкретном примере. Пусть требуется построить аксонометрическую проекцию (прямоугольную изометрию) кольца (рис. 316,а). Построения выполняем в следующей последовательности:

1) строим эллипс с⁰ - аксонометрическую проекцию окружности с (ACBD);

2) из произвольных точек эллипса с⁰, О⁰₁,О⁰₂, О⁰₃, ..., О⁰_n, (∀ О⁰_j; О⁰_j ∈ с⁰) проводим окружности b_j радиусом r - аксонометрические проекции вписанных сферических поверхностей β;

3) огибающие d⁰ и d⁰₂ окружностей b_j являются видимым очерком аксонометрической проекции кольца (рис. 316,6)