Определение рационального машинного алгоритма
ТеорияРешение одной и той же задачи может быть осуществлено различными графическими способами, каждому из которых соответствует свой машинный алгоритм. Возникает вопрос, какому из них отдать предпочтение? Чтобы ответить на этот вопрос, достаточно сопоставить между собой "схемы счета" сравниваемых алгоритмов.
Сравнение осуществляется путем подсчета суммарного числа машинных операций (команд), которые необходимо выполнить для реализации алгоритма на ЭЦВМ. С этой целью в графе 3 табл. 10 указано число команд, которые должна выполнить машина для реализации перечисленных в таблице стандартных операторов.
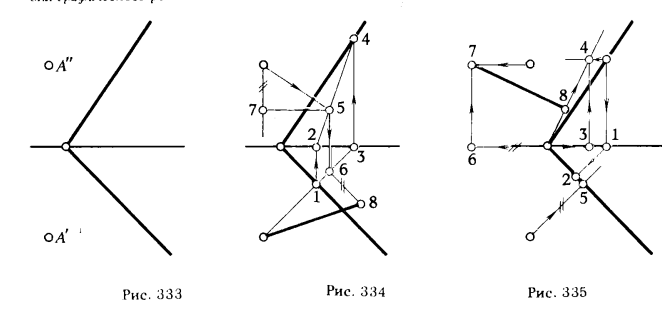
Поясним сказанное на примере: пусть требуется определить расстояние от точки А до плоскости α(рис. 333).
Эта задача может быть решена различными способами, в том числе и теми, что представлены на рис. 334 и 335. В первом случае решение осуществляется без применения способов преобразования (рис. 334).
Во втором плоскость общего положения а переведена во фронтально проецирующее положение с помощью перемещения || π1 (рис. 335). Выясним, какое решение требует меньшей затраты машинного времени. Для этого составим схемы счета для каждого варианта решения.
Схема счета, отражающая логику графического решения задачи, без применения способов преобразования будет иметь вид
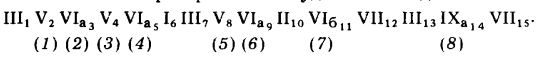
Схема счета решения этой же задачи с применением способа параллельного перемещения может быть записана:
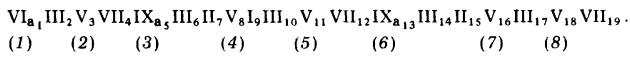
Подставив число команд, которые необходимо выполнить для каждого оператора, и суммировав их, мы получим: для первого варианта — 195 команд, для второго варианта — 278. Если условно принять, что время выполнения одной команды одинаково для различных команд, то можно сделать вывод, что первый вариант решения лучше. Машина затратит на 30% меньше времени, чем решая эту же задачу по второму варианту. Что касается точности решения, то в обоих случаях она будет одинаковой (определяется точностью задания исходных данных).
Уместно отметить, что, переходя на машинный метод решения задач, мы обнаруживаем, что не все те способы решения, которым следовало отдать предпочтение при решении задачи "вручную", оказываются удобными для машины. И наоборот, громоздкий, нерациональный способ, если он выполняется с помощью линейки и циркуля, может дать весьма рациональное машинное решение, т. е., переходя на машинный способ решения, образно говоря, необходимо произвести "переоценку ценностей".
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
- Перечислите основные вопросы, которые должны быть решены для осуществления автоматизации процесса графического решения задач.
- Нарисуйте структурную схему установки, включающую ЭЦВМ, которая обеспечивает комплексную автоматизацию процесса графического решения задач, и дайте объяснение назначения всех элементов, входящих в схему.
- Что подразумевается под термином "машинное чтение чертежа"?
- Каким образом осуществляется выявление растрэлементов, принадлежащих линии чертежа, и как определяется значение координат этих растрэлементов?
- Каким требованиям должен отвечать машинный метод решения задач, исходные данные которых представлены в графической форме?
- В чем сущность машинного метода решения задач?
- Что такое стандартный оператор?
- Что такое схема счета и что служит основанием для ее составления?
- Составьте схему счета для машинного решения задач:
- Как определяется рациональный машинный алгоритм?
- Определите, какой способ решения задачи по нахождению расстояния между скрещивающимися прямыми будет наиболее целесообразным для машины:
а) определить расстояние между двумя плоскостями;
б) определить точки встречи прямой с поверхностью прямого конуса, цилиндра, сферы;
в) найти линию пересечения поверхностей сферы и кругового цилиндра, ось которого не проходит через центр сферы.
а) без способов преобразования;
б) с использованием способа замены плоскостей проекций;
в) способом параллельного перемещения.