Центральное проецирование

Сущность центрального проецирования заключается в следующем: пусть даны плоскость π₁ и точка S (S∉π₁ рис. 5). Возьмем произвольную точку А (А ∉π₁, A≠S). Через заданную точку S и точку А проводим прямую (SA) и отмечаем точку А', в которой эта прямая пересекает плоскость π₁. Плоскость π₁ называют плоскостью проекции, точку S - центром проекции **, полученную точку А' - центральной проекцией точки А на плоскость π₁ , прямую (SA) - проецирующей прямой. Положения плоскости π₁ и центра S определяют аппарат центрального проецирования. Если он задан, то всегда имеется возможность определить положение центральной проекции любой точки пространства на плоскости проекции.

Действительно, пусть дана произвольная точка В (см. рис. 5); проведя проецирующую прямую (SB) и найдя точку ее встречи (пересечения) с плоскостью π₁ , определяем центральную проекцию В' точки

* По аналогии с плоскостью евклидова пространства, в котором плоскость можно рассматривать как множество точек (собственных), которые пересекаются прямой в одной (собственной) точке и плоскостью по одной (собственной) прямой.

** В некоторых учебниках встречается определение точки S как полюса проекции или как вершины конической поверхности. В этих случаях проекции называют соответственно полярными или коническими.

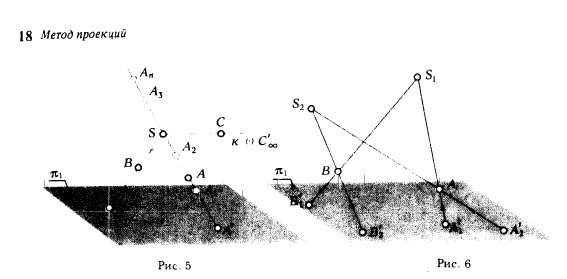
В при данном аппарате проецирования (фиксированном положении π₁ и S).

В том случае, когда точка С принадлежит плоскости, проходящей через центр проекции и параллельной плоскости π₁ , проецирующая прямая (SC) пересечет плоскость проекции в несобственной точке С'_∞. Таким образом, можно сделать вывод, что при заданном аппарате проецирования каждая точка пространства имеет только одну центральную проекцию. Это утверждение вытекает из того, что через две различные точки можно провести только одну прямую. К сожалению, обратное утверждение - каждой центральной проекции точки однозначно соответствует точка, не имеет места.

Из рис. 5 видно, что точка А' может быть центральной проекцией любой точки А₁, А₂, А₃, ... , А_n, принадлежащей прямой (A'S). Поэтому одна центральная проекция точки не дает возможности судить о положении самой точки в пространстве.

Для определения положения точки необходимо иметь две ее центральные проекции, полученные из двух различных центров. Имея две центральные проекции точки А'₁ и А'₂, полученные из центров S₁ и S₂ (рис. 6), можно определить положение точки А в пространстве. Для этого достаточно провести прямые (A'₁S₁ ) и (A'₂S₂) и отметить точку их пересечения.

На рис. 6 показано также определение положения точки В по заданным проекциям В'₁ и В'₂.