Инвариантные свойства ортогонального проецирования

Геометрические фигуры проецируются на плоскость проекции в общем случае с искажением. При этом характер искажений зависит от аппарата проецирования и положения проецируемой фигуры по отношению к плоскости проекции. В частности, при ортогональном проецировании, если проецируемая фигура занимает произвольное положение по отношению к плоскости проекции, ее проекция не сохраняет метрических характеристик оригинала - происходит искажение линейных и угловых величин.

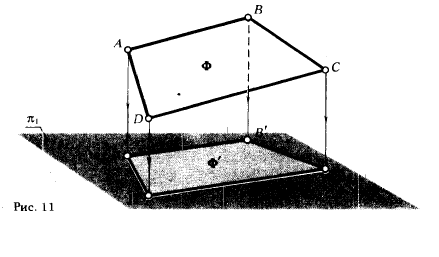
Действительно, при ортогональном проецировании трапеции ABCD на плоскость π₁, не параллельную плоскости трапеции (рис. 11), длины ее сторон, величины углов при вершинах, площадь и другие метрические характеристики оригинала на проекции A'B'C'D' не сохраняются.

Наряду с этим между фигурой-оригиналом и ее ортогональной проекцией на плоскость существует определенная связь, заключающаяся в том, что некоторые свойства проецируемой фигуры Ф сохраняются и на ее проекции Ф'.

Из рис. 11 видно, что точки А, В, С, D - вершины проецируемой трапеции (фигура Ф) проецируются в точки А', В', С', D' - вершины трапеции-проекции (фигура Ф'); отрезки [АВ], [ВС], [CD], [DA] - стороны трапеции проецируются в отрезки [А'В'], [В'С'], [C'D'], [D'A'] - стороны трапеции-проекции.

Параллельным основаниям [АВ] || [DC] проецируемой трапеции соответствуют также параллельные основания- [А'В' ] || [D'C'] трапеции-проекции.

Свойства геометрических фигур, которые не изменяются в процессе проецирования, называются независимыми иди инвариантными относительно выбранного способа проецирования.

Основу любой геометрии составляет система аксиом. Любое геометрическое определение и предложение (теорема), равно как и доказательства теорем, базируются на принятой системе аксиом.

При ортогональном проецировании - получении проекций геометрической фигуры по ее оригиналу или при решении обратной задачи - определении формы и размеров оригинала по его ортогональным проекциям базируются на инвариантных свойствах ортогонального проецирования:

1. Ортогональная проекция точки есть точка:

А → А'

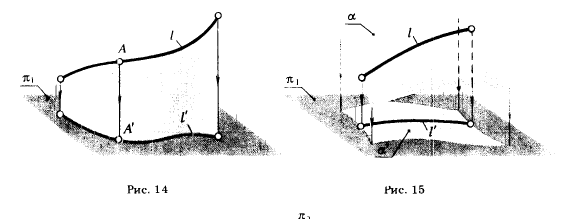
2. Если фигура Ф₁ принадлежит фигуре Ф, то ортогональная проекция фигуры Ф'₁ принадлежит ортогональной проекции фигуры Ф'*:

Ф₁⊂Ф⇒Ф'₁⊂Ф'.

Из свойства 1 получаем:

1 а. Ортогональная проекция прямой на плоскость есть прямая, в частном случае, когда прямая перпендикулярна плоскости проекции, - точка (рис. 12 и 13) :

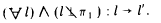
Действительно, возьмем на прямой l (рис. 12) ряд точек 1, 2, 3, ... ... , n и проведем через них проецирующие прямые а₁, а₂, а₃, ... , а_n, перпендикулярные плоскости π₁. Каждая из этих прямых пересечет плоскость π₁ в точках 1', 2' 3' ... , n' .

Множество всех прямых {a_l, а₂, а₃,... }, проходящих через нетождественные точки прямой l перпендикулярно к плоскости π₁, образуют проецирующую плоскость α, которая пересекается с плоскостью π₁ по прямой, поэтому точки 1', 2', 3', ...,n' (ортогональные проекции точек 1, 2, 3, ...,n прямой l) принадлежат одной прямой l' - ортогональной проекции прямой l.

На рис. 13 показан случай, когда прямая l⊥π₁ . Из чертежа видно, что все прямые {а₁, а₂, а₃, ... ,а_n} проецирующие точки 1, 2, 3, ... , n прямой l, совпадают с этой прямой и пересекают плоскость в одной точке 1' ≡ 2' ≡ 3' ≡ ... ≡ n' - горизонтальной проекции прямой l'**.

Из свойства 2 следует:

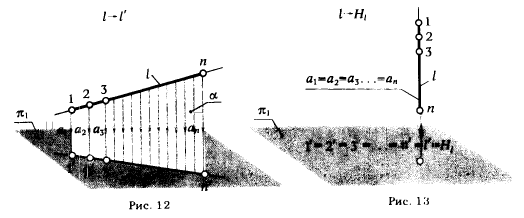
2 а. Если точка А принадлежит линии l, то ортогональная проекция точки А' принадлежит ортогональной проекции линии l' (рис. 14) :

А∈l⇒A'∈l'.

2 б. Если линия l принадлежит поверхности α, то ортогональная проекция линии l' принадлежит ортогональной проекции поверхности α' (рис. 15):

l⊂α ⇒l'⊂α'.

* С позиции теории множеств это свойство можно сформулировать иначе: "если множество М принадлежит (является подмножеством) множеству N, то ортогональная проекция множества М' на плоскость принадлежит ортогональной проекции N' на эту же плоскость.

**На рис. 13 горизонтальная проекция прямой l' обозначена H_l, так как в этом случае l' ≡ Н_l.

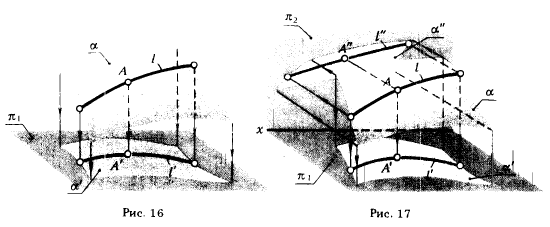
2 в. Если точка А принадлежит поверхности α, то ортогональная проекция точки А' находится на ортогональной проекции линии l', принадлежащей ортогональной проекции поверхности α' (рис. 16):

A ∈ α ⇒ A' ∈ l'⊂ α'.

В том случае, когда удовлетворяется условие принадлежности А" ∈ l" и А" ∈ l" ⊂ α" на другой плоскости проекции π₂ (π₂∦π₁), справедливы следующие утверждения:

А ∈ ⇔ (А' ∈ l')∧(А" ∈ l");

A ∈ l ⊂ α ⇔ (А' ∈ l' ⊂ α') ∧ (А" ∈ l" ⊂ α").

Поставленные здесь знаки эквивалентности между левой и правой частями показывают, что справедливы и обратные утверждения:

- если ортогональные проекции точки А (А' и А") принадлежат соответственно ортогональным проекциям линии l (l' и l"), то точка А принадлежит линии l;

- если ортогональные проекции точки А (А' и А") принадлежат соответствующим ортогональным проекциям линии l(l' и l"), которые, в свою очередь, принадлежат одноименным ортогональным проекциям поверхности α (α' и α"), то точка А принадлежит поверхности α (рис. 17).

2 г. Если фигура Ф принадлежит плоскости α, перпендикулярной плоскости проекции π₁, то ортогональная проекция этой фигуры принадлежит линии пересечения плоскости α с плоскостью π₁ - горизонталь

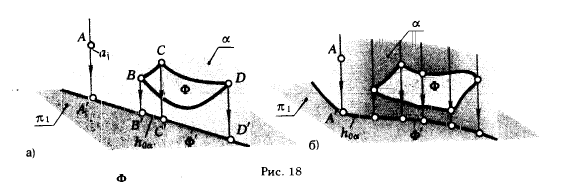
ному следу h_оα плоскости α: (Ф ⊂ α)∧(α ⊥ π₁ ) = Ф' ⊂ h_оα

В справедливости этого утверждения легко убедиться, рассматривая рис. 18, а. Пусть α - плоскость, перпендикулярная плоскости проекции π₁. Плоскость α можно рассматривать как состоящую из множества прямых{a₁,а₂, а₃, ... , а_n } , перпендикулярных π₁ , каждая из которых пересекает плоскость π₁ в точке, принадлежащей прямой h_oα.

Допустим, что в плоскости α задана точка А (А ∈ а). Очевидно, горизонтальная проекция может быть найдена как результат пересечения прямой c_j с плоскостью π₁ (a_j ∋ А и a_j ⊂ α и a_j ⊥ π₁ ), но из свойства 1а (см. рис. 13) следует, что a_j ∩ π₁ = А' ∈ h_oα.

Если в плоскости α будет задана какая-либо фигура Ф, то, проецируя точки В, С, D, ... этой фигуры на плоскость π₁, мы каждый раз будем получать горизонтальные проекции этих точек, принадлежащие следу h_оα плоскости α. Совокупность горизонтальных проекций точек В', С', D', ... укажет горизонтальную проекцию фигуры Ф', т. е. Ф' ⊂ h_0α.

Из рис. 18,6 видно, что отмеченное свойство сохраняется и в том случае, когда вместо плоскости будет взята произвольная горизонтально проецирующая поверхность.

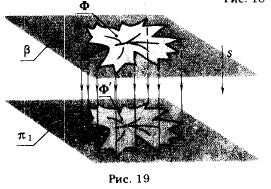
2 д. Если фигура Ф принадлежит плоскости β, параллельной плоскости проекции π₁, то ортогональная проекция этой фигуры на плоскость π₁ конгруентна самой фигуре (рис. 19) :

(Ф ⊂ β)∧(β || π₁) ⇒ Ф' ≅ Ф.

В справедливости этого свойства ортогонального проецирования легко убедиться путем следующих рассуждений: представим, что плоскость β совпадает с плоскостью проекций π₁ (частный случай параллельности). Не вызывает сомнений, что ортогональная проекция фигуры Ф' на плоскость π₁ ничем не будет отличаться от самой фигуры Ф.

Если плоскость β будет перемещаться вдоль проецирующего луча s, оставаясь при этом параллельной своему первоначальному положению (плоскости π₁ ), то это не повлечет за собой изменения формы и размеров проецируемой фигуры.

2 е. Следует иметь в виду, что в том случае, когда проецируемой фигурой является прямой угол, для получения неискаженной ортогональной проекции этого угла достаточно, чтобы только одна из его

сторон была параллельна плоскости проекции (при условии, что другая сторона угла не перпендикулярна плоскости проекции). Это свойство может быть записано:

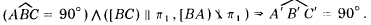
Если ∠ABC прямой и сторона ВС этого угла параллельна плоскости проекции π₁, а сторона ВА не перпендикулярна плоскости π₁, то ортогональная проекция угла на плоскость.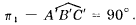

В большинстве учебников по начертательной геометрии это инвариантное свойство ортогонального проецирования предлагается в виде теоремы о частном случае проецирования прямого угла. Ниже приводится одно из возможных доказательств этой теоремы, взятое нами из учебника В. О. Гордона и М. А. Семенцова-Огиевского.

Положим, что сторона ВС прямого угла ABC (рис. 20) параллельна плоскости проекции π₁ . В этом случае прямая ВС параллельна В'С'.

Пусть вторая сторона прямого угла, наклонная АВ, пересекает свою проекцию А'В' в точке К. Проведем в плоскости проекции через точку К прямую KL параллельно В'С'. Прямая KL также параллельна ВС и ∠B'KL получается прямым. Согласно теореме о трех перпендикулярах ∠KBC также прямой. Следовательно, и ∠A'B'C' будет прямым.

Отмеченные инвариантные свойства имеют чрезвычайно важное значение при решении позиционных (свойства 2 а ... 2 г) и метрических (свойства 2 д и 2 е) задач.

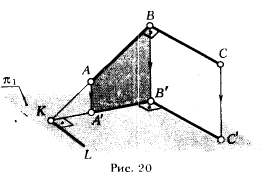
2 ж. Если точка К есть результат пересечения прямых а и b, то ортогональная проекция этой точки К' определяется пересечением ортогональных проекций прямых а' и b' (рис. 21).

К этому свойству можно прийти путем следующих рассуждений. Допустим нам даны две фигуры Ф₁ и Ф₂. Обозначим фигуру, получающуюся в результате их пересечения, Ф₃. Тогда Ф₃ = Ф₁ ∩ Ф₂, но Ф₃ ⊂ Ф₁ и Ф₃ ⊂ Ф₂, на основании аксиомы 2 можно записать:

Ф'₃ ⊂ Ф'_{1 и Ф'3 ⊂ Ф'2}

т. е.

Ф₃ = Ф₁ ∩ Ф₂ ⇒ Ф', = Ф'₁ ∩ Ф'₂.

Если в качестве фигуры Ф₁ будет задана прямая а, а вместо фигуры Ф₂ - прямая b (пересечение прямых а и b - точка К), то мы придем к заключению, которое требовалось доказать:

К = a ∩ b ⇒ К' = а' ∩ b'.

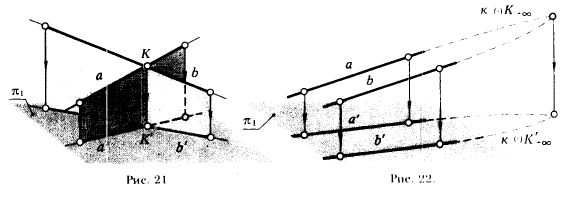
В том случае, когда а || b, точкой пересечения прямых а и b будет бесконечно удаленная (несобственная) точка K_∞ ,которая при ортогональном проецировании на плоскость π₁ спроецируется также в несобственную точку К'_∞; следовательно, а'||b'. Это свойство можно записать:

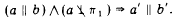
2 з. Если прямые а и b параллельны между собой и не перпендикулярны плоскости проекции π₁, то параллельны и их ортогональные проекции на эту плоскость (рис. 22). Приведенный инвариант позволяет сформулировать еще два свойства, инвариантные относительно ортогонального проецирования.

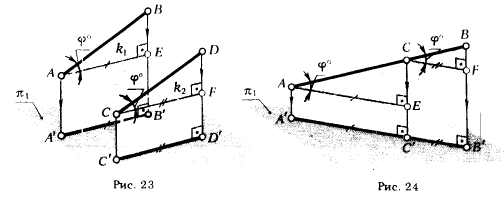
2 и. Если отрезок [АВ] параллелен отрезку [CD], то отношение длин отрезков равно отношению длин их ортогональных проекций (рис. 23) *:

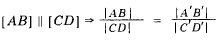
2 к. Если точка С принадлежит отрезку [АВ], то отношение [АС] к [СВ] равно отношению их проекций. Или иначе, если точка С делит отрезок в данном отношении, то и проекция С' (или С") делит проекции отрезка в том же отношении (рис. 24) :

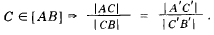
Справедливость двух последних утверждений ясна из рис. 23 и 24 и не нуждается в доказательстве.