Положения плоскости относительно плоскостей проекций

Возможны следующие положения плоскости относительно плоскостей проекций π₁, π₂, π₃: 1) плоскость не перпендикулярна ни к одной из плоскостей проекций, 2)плоскость перпендикулярна лишь к одной из них, 3) плоскость перпендикулярна к двум плоскостям проекций.

Плоскости второго и третьего положений носят общее название «проецирующие плоскости».

1.Плоскость, не перпендикулярная ни к одной из плоскостей проекций, является плоскостью общего положения (см, рис, 105).

Рассмотрим, например, плоскость, изображенную на рис. 112,

Эта плоскость не перпендикулярна ни к π₁, ни к π₂, ни к π₃. То, что она не перпендикулярна ни к π₁, ни к π₂, подтверждается видом проекций А'В'С' и А"В"С": если бы плоскость, определяемая треугольником АВС, была перпендикулярна хотя бы к π₁ то (рис, 120) проекция А'В'С' представляла бы собой отрезок прямой.

Итак, рассматриваемая нами плоскость не перпендикулярна ни к π₁, ни к π₂. Но, может быть, эта плоскость перпендикулярна к π₃? Нет, горизонталь этой плоскости АК не перпендикулярна к π₃ (сравните с рис. 54, где показана прямая, перпендикулярная к π₃), и, следовательно, пл, АВС не перпендикулярна к π₃.

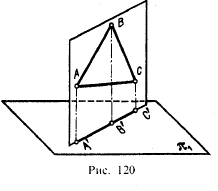
Итак, на рис, 112 дан пример задания плоскости общего положения в системе π₁, π₂.

Другими примерами задания плоскости общего положения служат рис. 109, 110, 111, 113, 116, а также рис. 102, 104, 107, слева, 108, 115, справа, 117, 119, на которых плоскости выражены следами. Плоскость общего положения (см. рис. 105) пересекает каждую из осей х, у, z. Следы плоскости общего положения никогда не перпендикулярны к этим осям проекций.

Если следы плоскости общего положения h'_0α и f"_0α образуют с осью х одинаковые углы, то это означает, что углы между пл.α и плоскостями π₁, и π₂ равны между собой. Действительно, если плоские углы трехгранного угла равны между собой, то равны и лежащие против них двугранные углы; углы, образуемые следами h'_0α и f"_0α с осью х (см. рис. 105), представляют собой плоские углы, против которых соответственно расположены двугранные углы, образуемые пл. α с плоскостями π₂ и π₁.

Если плоскость общего положения должна быть одинаково наклонена к плоскостям π₁, π₂ и π₃, то (см. рис. 105), очевидно, ОХ_α=ОУ_α=OZ_α т. е. следы составляют с осями проекций углы 45°.

Рассматривая плоскость общего положения в пространстве в пределах первой четверти или первого октанта, замечаем, что угол между горизонтальным и фронтальным следами может быть острым (см. рис. 105) или тупым (рис. 121).

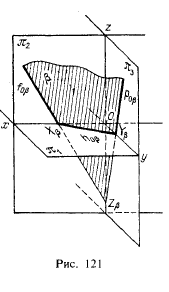
Пл. β, изображенная на рис. 121, проходит через все октанты, кроме шестого.

Если чертеж плоскости общего положения строить по координатам точек пересечения следов, то, очевидно, на рис. 121 должны быть заданы положительные абсциссы и ордината точек X_β и Y_β и отрицательная аппликата точки Z_β.

На рис. 122 изображен частный случай плоскости общего положения — ее следы h'_0α и f"_0α на чертеже лежат на одной прямой. Вспоминая схему совмещения плоскостей проекций (рис. 15 на с. 17), заметим, что следы h'_0α и f"_0α образуют равные углы с осью х не только на чертеже, но и в пространстве. Как показано на рис. 122 справа, из равенства прямоугольных треугольников КК'Х_α, и К"К'Х_α, следует, что угол КХ_αК' равен углу К'Х_αК", т. е. след f"_0α, образует с осью х такой же угол, как и след h'_0α.

Отсюда пл. α образует равные углы с плоскостями π₁ й π₂. Часть пл. α, находящаяся в первой четверти, содержит в себе натуральный угол между h'_0α и f"_0α (в нашем примере — тупой).

На рис. 122 показано также построение третьего следа плоскости (р_0α) по заданным двум ее следам h'_0α и f"_0α. Вследствие того, что следы h'_0α и f"_0α лежат на одной прямой, точка Z_α сливается с точкой Y_α, и, следовательно, точка У_1α, оказывается на таком же расстоянии от точки О, на каком находится точка Z_α; поэтому след р"'_0α наклонен под углом 45° к оси у (и к оси z); именно такой наклон профильного следа будет получаться во всех случаях построения

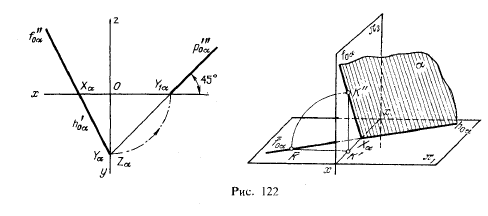
плоскости, у которой на чертеже горизонтальный и фронтальный следы лежат на одной прямой, пересекающей ось х под острым углом.

Такая плоскость проходит через перпендикуляр к оси х, составляющий с пл. π₂ (или с яд) угол 45°. А так как этот перпендикуляр является перпендикуляром к биссекторной плоскости двугранных углов, смежных с углом π₁π₂, то рассматриваемая плоскость может быть определена как плоскость, перпендикулярная к биссекгорной плоскости второй и четвертой четвертей пространства ¹).

¹) Интересующихся более подробным изложением отсылаем к предыдущим изданиям этой книги.

2.Если плоскости перпендикулярны лишь к одной из плоскостей проекций, то возможны три случая частных положенйй.

а)Плоскость перпендикулярна к горизонтальной плоскости проекций. Такие плоскости называются горизонтально-проецирующими.

Пример дан на рис. 123: плоскость задана проекциями треугольника АВС. Горизонтальная проекция представляет собой отрезок прямой линии. Угол φ₂ равен углу между заданной плоскостью и пл. π₂.

На рис. 124 дан пример изображения горизонтально-проецирующей плоскости ее следами: слева дано наглядное изображение, в середине — чертеж в системе

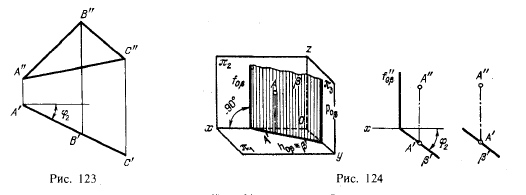
π₁, π₂ с указанием оси х и следов f"_0β и h'_0β, справа — без указания оси х и, следовательно, следа f"_0β.

Фронтальный след перпендикулярен к пл. π₁ и к оси проекций х. Горизонтальный же след может составлять с осью проекций любой угол; этот угол служит линейным углом двугранного между горизонтально-проецирующей плоскостью и пл. π₂.

Угол между h_0β и f_0β, а также угол между h_0β и p_0β в пространстве равен 90°.

Если в горизонтально-проецирующей плоскости расположена точка, то ее горизонтальная проекция должна быть на горизонтальном следе плоскости. Это относится и к любой системе точек, расположенных в горизонтально-проецирующей плоскости, будь то прямые линии, плоские кривые или фигуры.

След h_0β≡β' можно рассматривать как горизонтальную проекцию плоскости.

б)Плоскость перпендикулярна к фронтальной плоскости проекций. Такие плоскости называются фронтально-проецирующими.

Пример дан на рис. 125: плоскость задана проекциями треугольника DEF. Фронтальная проекция представляет собой отрезок прямой линии. Угол φ₁ равен углу между DEF и пл. π₁.

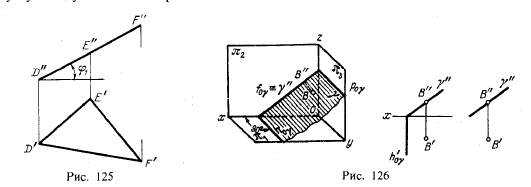
На рис. 126 слева дано наглядное изображение, в середине — чертеж в системе π₁, π₂ с указанием оси проекций, справа — без указания оси проекций. Горизонтальный след перпендикулярен к пл. π₂ и к оси проекций. Фронтальный же след может составлять с осью проекций любой угол; этот угол служит линейным углом двугранного между фронтально-проецирующей плоскостью и пл. π₂.

Угол между f_0γ и h_0γ в пространстве равен 90°.

Если в фронтально-проецирующей плоскости расположена точка, то ее фронтальная проекция должна быть на фронтальном следе плоскости. Это относится и к любой системе точек. След f_0γ≡γ" (рис. 126) можно рассматривать как фронтальную проекцию пл. γ.

в)Плоскость перпендикулярна к профильной плоскости проекций. Такие плоскости называются профилъно-проецирующими.

На рис. 127 дан пример профильно-проецирующей плоскости: плоскость задана проекциями треугольника АВС. Горизонталь этой плоскости расположена перпендикулярно к пл. π₃: проекции A"D" и A'D' взаимно параллельны. Это служит признаком того, что перед нами профильно-проецирующая плоскость, а не плоскость общего положения (сравните с рис. 112).

Профильная проекция треугольника АВС представляет собой отрезок прямой линии. Угол φ₁ между этим отрезком и линией связи С"С"' равен углу наклона

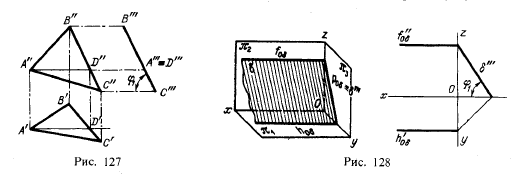
плоскости треугольника к пл. π₁ а угол наклона плоскости треугольника к пл. π₂ равен 90° — φ₁.

На рис. 128 дан пример изображения профильно-проецирующей плоскости ее следами.

Горизонтальный и фронтальный следы этой плоскости параллельны оси х и, следовательно, параллельны между собой.

Изображенная на рис. 107 справа плоскость также является профильно-проецирующей.

Плоскость, перпендикулярная к одной из плоскостей проекций (горизонтально-, фронтально- или профильно-проецирующая), может, в частности, проходить через ось проекций, Такую плоскость дополнительно называют осевой плоскостью.

Рассмотрим, например, осевую профильно-проецирующую плоскость (рис. 129). Следы ее f_0σ и h_0σ, сливаются с осью х; в этом случае необходимо иметь еще третий ее след p_0σ≡σ"' или хотя бы положение одной точки, принадлежащей этой плоскости и не лежащей на оси х.

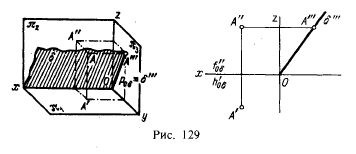
Осевая плоскость может быть биссекторной; это значит, что осевая плоскость делит двугранный угол, образованный плоскостями проекций пополам.

Как можно изобразить профильно-проецирующую плоскость на чертеже без осей проекций? Так, как дано на рис. 127. Другой пример представлен на рис. 130: плоскость задана двумя пересекающимися прямыми, из которых одна (АВ) перпендикулярна к пл. π₃, а другая занимает произвольное положение.

3. Если плоскости перпендикулярны к двум плоскостям проекций, то также возможны три случая частных положений ¹).

а)Плоскость перпендикулярна к плоскостям π₂ и я3, т. π₃ параллельна плоскости π₁. Такие плоскости называются горизонтальными.

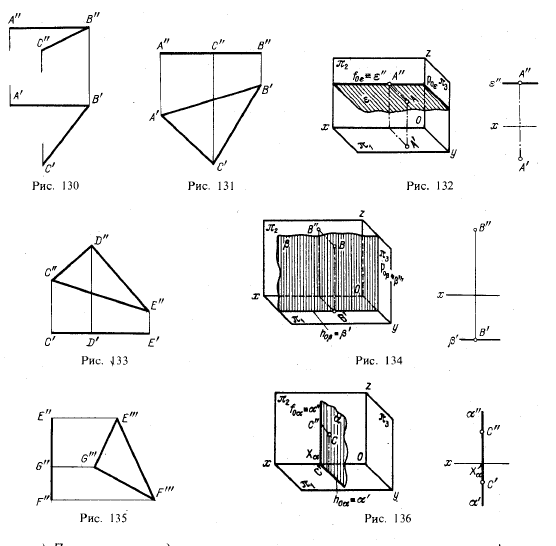
На рис. 131 дан пример горизонтальной плоскости, заданной проекциями треугольника АВС. На рис. 132 справа изображена горизонтальная плоскость в системе π₁, π₂ при помощи фронтального следа. След (f_0ε≡ = ε") можно рассматривать как фронтальную проекцию плоскости.

б)Плоскость перпендикулярна к плоскостям π₁ и π₃, т. е. параллельна плоскости π₂. Такие плоскости называются фронтальными.

На рис. 133 дан пример фронтальной плоскости, заданной проекциями треугольника CDE.

¹) Для таких плоскостей встречается общее название «плоскости уровня». Однако это название отвечает обычному представлению только о горизонтальности.

На рис. 134 справа дан пример изображения фронтальной плоскости в системе π₁, π₂ при помощи следа (h_0β≡β'), который можно рассматривать как проекцию этой плоскости на пл. π₁.

в)Плоскость перпендикулярна к плоскостям π₁ и π₂, т. е. параллельна плоскости π₃. Такие плоскости называются профильными.

Пример изображения в системе π₂, π₃ дан на рис. 135: плоскость задана проекциями треугольника EFG.

На рис. 136 дан пример изображения в системе π₁, π₂ при помощи следов. Каждый из них можно рассматривать как проекцию плоскости α а на соответствующей плоскости проекций. Профильная плоскость сочетает в себе свойства фронтально- и горизонтально-проецирующей плоскостей.

Вопросы к § 19

1. Как располагаются в системе π₁, π₂, π₃ плоскость общего положения и плоскости, называемые проецирующими?
2. Что такое фронтально-нроецирующая плоскость, горизонтально-проецирующая, профильно-проецирующая?
3. Как определить, является ли плоскость, заданная в системе π₁, π₂ пересекающимися или параллельными прямыми, плоскостью общего положения или профильно-проецирующей?
4. Что представляет собой горизонтальная проекция горизонтально-проецирующей плоскости и фронтальной плоскости?
5. Тот же вопрос в отношении фронтальной проекции фронтально-проецирующей плоскости и горизонтальной плоскости.
6. Где располагается горизонтальная проекция любой системы точек, расположенной в горизонтально-проецирующей или фронтальной плоскости?
7. Где располагается фронтальная проекция любой системы точек, расположенной в горизонтальной или фронтально-проецирующей плоскости?
8. Чему равен в пространстве угол между фронтальным и горизонтальным следами горизонтально- и фронтально-проецируюшей плоскостей?