Основы способа вращения
ТеорияПри вращении вокруг некоторой неподвижной прямой (ось вращения) каждая точка вращаемой фигуры перемещается в плоскости, перпендикулярной к оси вращения (плоскость вращения). Точка перемещается по окружности, центр которой находится в точке пересечения оси с плоскостью вращения (центр вращения), а радиус окружности равняется расстоянию от вращаемой точки до центра (это радиус вращения). Если какая-либо из точек данной системы находится на оси вращения, то при вращении системы эта точка считается неподвижной.
1) Подробное изложение способа вращения дал в свое время В.И.Курдюмов в книге «Курс начертательной геометрии», в отделе, посвященном ортогональным проекциям.
Ось вращения может быть задана или выбрана; в последнем случае выгодно расположить ось перпендикулярно к одной из плоскостей проекций, так как при этом упрощаются построения.
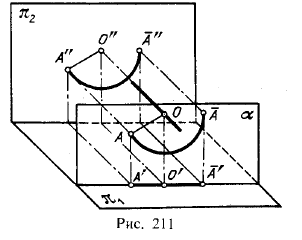
Действительно, если ось вращения перпендикулярна, например, к пл.π2, то плоскость, в которой происходит вращение точки, параллельна пл. π2. Следовательно, траектория точки проецируется на пл. π2 без искажения, а на пл. π1 — в виде отрезка прямой линии (рис. 211).