Вращение точки, отрезка прямой, плоскости вокруг оси, параллельной плоскости проекций, и вокруг следа плоскости
ТеорияПоворот плоской фигуры вокруг ее горизонтали. Для определения формы и размеров плоской фигуры можно ее повернуть вокруг принадлежащей ей горизонтали так, чтобы в результате вращения фигура расположилась параллельно плоскости π1.
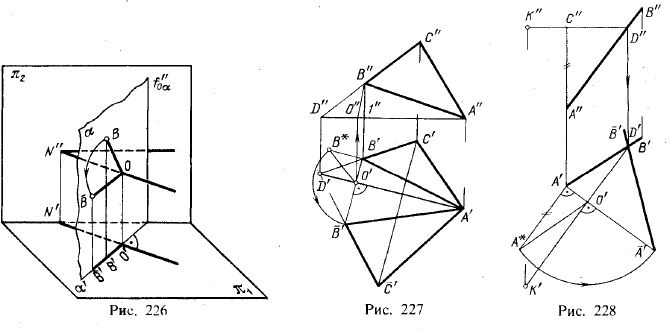
Рассмотрим сначала поворот точки (рис. 226). Точка В вращается вокруг некоторой горизонтально расположенной оси ON", описывая дугу окружности, лежащую в пл. α. Эта плоскость перпендикулярна к оси вращения и, следовательно, является горизонтально-проецирующей; поэтому горизонтальная проекция окружности, описываемой точкой В, должна находиться на α'.
Если радиус ОВ займет положение, параллельное пл. π1 то проекция О'B' окажется равной ОВ, т. е. равной натуральной величине радиуса ОВ.
Теперь рассмотрим рис. 227. На нем показан поворот треугольника АВС. В качестве оси вращения взята горизонталь AD. Точка А, расположенная на оси
1) Получающаяся при этом проекция куба на пл. π2 (рис. 225) совпадает с изображением куба в прямоугольной изометрической проекции, изучаемой в курсе черчения средней школы.
вращения, останется на месте. Следовательно, для изображения горизонтальной проекции треугольника после поворота надо найти положение проекций других двух его вершин. Опуская из точки В' перпендикуляр на A'D', находим горизонтальную проекцию центра вращения — точку О' и горизонтальную проекцию радиуса вращения точки В — отрезок О'В', а затем фронтальную проекцию центра вращения — точку О" и фронтальную проекцию радиуса вращения точки В — отрезок 0"В". Теперь надо определить натуральную величину радиуса вращения точки В. Для этого применен способ, указанный в § 13, т. е. построение прямоугольного треугольника. По катетам О'В' и В'В* = В"1" строим прямоугольный треугольник О'В'В*, гипотенуза его равна радиусу вращения точки В.
Теперь можно найти положение точки B', а затем точки С', причем не определять радиус вращения точки С, а найти положение точки С' в пересечении двух прямых, из которых одна является перпендикуляром, проведенным из точки С' к прямой A'D', а другая проходит через найденную точку B' и точку D' (горю зонтальную проекцию точки D, принадлежащей стороне ВС и расположенной на оси вращения).
Проекция А'B'С' выражает натуральную величину ΔАВС, так как после поворота плоскость треугольника параллельна пл. π1. Фронтальная же проекция треугольника совпадает с фронтальной проекцией горизонтали, т. е. представляет собой прямую линию.
На рис. 227 дано построение для случая, когда горизонталь проведена вне проекций треугольника. Это позволяет избежать наложения проекций одной на другую, но чертеж занимает большую площадь.
Если требуется повернуть плоскую фигуру до положения параллельного пл. π2, то за ось вращения надо выбрать фронталь.
Обратим внимание на то, что в построении, показанном на рис. 226, фронтальная проекция радиуса вращения точки В не участвует. Очевидно, поняв сущность построения, можно не строить этой проекции. Пример дан на рис. 228, где показан поворот плоскости, заданной точкой К и прямой АВ, до положения, параллельного пл. π1. Поворот совершен вокруг горизонтали KD. Горизонталь проведена через точку К, которая, следовательно, останется «неподвижной». Остается повернуть прямую АВ вокруг KD, точнее, повернуть, например, только точку А, так как точка D на прямой АВ также «неподвижна»: она принадлежит оси вращения. Проведя А'О'⊥ K'D', т. е. наметив положение горизонтального следа той горизонтально-проецирующей плоскости, в которой находится и поворачивается точка А, получаем точку О' — горизонтальную проекцию центра вращения точки А и О'А' — горизонтальную проекцию радиуса вращения точки А. Теперь находим натуральную величину радиуса вращения RA как гипотенузу треугольника О'А'А*, в котором катет А'А*_= А"С". Найдя точку А' — горизонтальную проекцию точки А после поворота, проводим А'В' — горизонтальную проекцию прямой АВ после поворота, пользуясь точкой D'. Итак, мы обошлись без фронтальных проекций центра вращения и радиуса вращения.
Поворот плоскости вокруг ее следа до совмещения с соответствующей плоскостью проекций 1). Если плоскость вращать вокруг ее следа до совмещения с плоскостью проекций, в которой расположен этот след, то отрезки линий и фигуры, расположенные в плоскости, изобразятся без искажения. Очевидно, это построение аналогично по своему содержанию повороту плоскости вокруг ее горизонтали или фронтали до параллельности соответствующей плоскости проекций: следы плоскости можно рассматривать — горизонтальный след как «нулевую» горизонталь плоскости, фронтальный — как «нулевую» фронталь.
На рис. 229 показано совмещение плоскости общего положения α с плоскостью π1 причем поворот произведен вокруг h'0α в направлении от плоскости π2 к зрителю.
В положении совмещения с пл. π1 на пл. α окажутся две пересекающиеся прямые — след h'0α и прямая f"0α которая представляет собой след f"0α, совмещенный с пл. π1.
1) Этот случай известен также под названием «способ совмещения».
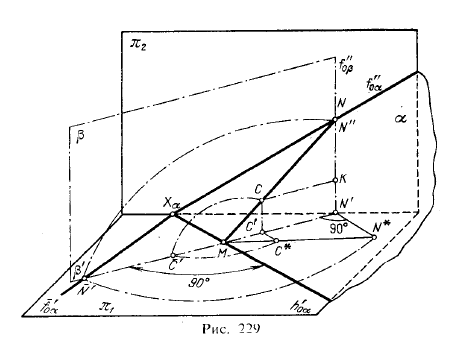
След h'0α как ось вращениπ1 не меняет своего положения; точка пересечения следов также не меняет своего положения, а потому, если бы требовалось указать совмещенное положение следа f"0α то достаточно было бы найти еще одну точку этого следа (кроме точки Xα) в положении совмещения в пл. π1. Найдем совмещенное положение какой-нибудь точки N, лежащей на следе f"0α. Эта точка опишет дугу окружности в пл. β, перпендикулярной к оси вращения; центр этой дуги лежит в точке М пересечения пл. β со следом h'0α. Описывая из точки М дугу радиусом MN в пл. β мы получаем в пересечении этой дуги с β' точку N' на пл. π1. Проведя через Xα, и N' прямую, получим f'0α. Так как отрезок XαN не изменяет своей величины при вращении плоскости, то, очевидно, точку N' можно получить в пересечении β' с дугой, описанной в пл. π1, из Хα радиусом XαN.
На чертеже (рис. 230) на следе f"0α выбрана произвольная точка N (она совпадает со своей проекцией N"); через ее проекцию N' проведена прямая N'M, перпендикулярная к оси вращения — следу h'0α. На этой прямой должна лежать точка N после совмещения с пл. π1 на расстоянии от точки М, равном радиусу вращения точки N, или на расстоянии XαN” от точки Хα. Длину радиуса вращения можно определить как гипотенузу прямоугольного треугольника с катетами MN' и N'N* (N'N* = N"N'). Проводя из точки М дугу радиуса MN* или из точки Xα дугу радиуса ХαN", получаем на прямой N'M совмещенное с пл. π1 положение точки N — точку N'. Проведя через точки Хα и N' прямую, получим совмещенное положение следа f"0α - прямую f'0α.
Вернемся к рис. 229 и рассмотрим на нем совмещение точки С с пл. π1
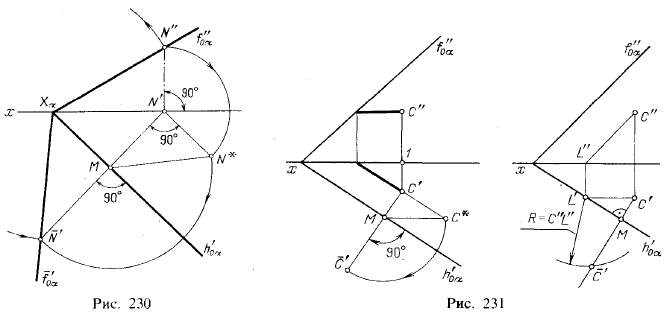
Нахождение совмещенного положения точки С с пл. π1 показано на рис. 231 слева. Через точку С' проведена прямая С'М, перпендикулярная к h'0α. Радиус вращения МС* найден как гипотенуза прямоугольного треугольника, у которого один катет СМ, а другой катет С'С* = С"1. Радиусом МС* проводим из точки М дугу и засекаем на продолжении прямой СМ точку С' — положение точки С в пл. π1.
Это построение можно выполнить и так, как показано на рис. 231 справа. Установив положение точки С в пл. α при помощи фронтали и проведя прямую С'М перпендикулярно к h'0α, засекаем эту прямую из точки L', как из центра, дугой, радиус которой равен отрезку С"L", т. е. натуральной величине отрезка CL в пл. α. В совмещении эта величина сохраняется: C'L' = СL
Если в плоскости дан отрезок прямой, то, найдя совмещенное положение концов этого отрезка, мы получаем натуральную величину отрезка.
Как известно, каждая горизонталь, взятая в пл. α, располагается параллельно h'0α, а фронталь — параллельно f"0α поэтому, если придется находить совмещенное положение горизонтали или фронтали, достаточно будет найти совмещенное положение их следа, через который и провести прямую, параллельную соответственно h'0α или f"0α (если пл. α совмещена с пл. π1)
Этим мы воспользуемся для обратного построения. Пусть задана точка С' — совмещенное с пл. π1 положение точки С; требуется найти проекции точки С, если она должна_лежать в пл. α, заданной следами (см. также рис. 229).
Когда точку С' «поднимают в пространство», то горизонтальная ее проекция — точка С' — перемещается по прямой СN' (рис. 232), перпендикулярной к h'0α т. е.
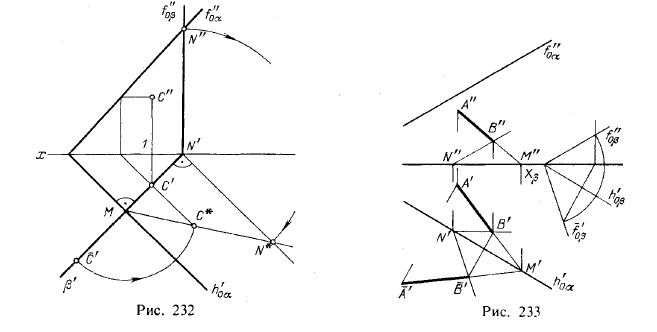
по следу β' плоскости вращения β. Точка С в пространстве должна лежать на линии пересечения плоскости α с плоскостью вращения (рис. 229) на расстоянии МС' от точки М.
Построим на пл. π1 прямоугольный треугольник MN'N*, у которого сторона N'N* = N"N' (рис. 232) и который, следовательно, равен треугольнику MN'N" в пространстве.
Откладывая на гипотенузе MN* от точки М отрезок МС' (радиус вращения), получаем точку С*. Проведя через нее прямую, перпендикулярную к MN', получим точку С' — искомое положение горизонтальной проекции точки С.
Точка С" должна находиться на перпендикуляре, проведенном из точки С' к оси х на расстоянии С"1, равном С'С*.
Если надо «поднять в пространство» отрезок прямой линии, то следует в общем случае поднять две его точки так, как это только что было указано, или использовать так называемую «неподвижную» точку. Это показано на рис. 233, где надо было «поднять в пространство» (т. е. на пл. α) отрезок АВ, заданный в совмещенном с пл. положении (A'B'). Построение несколько усложнено тем, что точка пересечения следов f"0α и h'0α считается недоступной.
Построена вспомогательная пл. β||α, и найден след f'0β совмещении с пл. π1. Так как β||α то f'0β определяет направление фронталей как пл. β, так и пл. α в совмещенном с пл. π1 положении. Поэтому, проведя B'N'||f'0β, получаем в совмещении с пл. π1 фронталь пл. α, на которой расположена в пространстве точка В. Построив проекции этой фронтали, находим на них проекции В' и В". Если же теперь продолжить прямую A'B' до пересечения в точке М' со следом h'0α, то на прямой, проходящей через эту «неподвижную» точку М' и через построенную проекцию В', расположится горизонтальная проекция А'В'. Проекция А"В" получится на прямой, проходящей через точки М" и В".
Нами рассмотрено совмещение плоскости с горизонтальной плоскостью проекций, причем вращение плоскости производилось вокруг горизонтального следа. Если требуется совместить ее с фронтальной плоскостью проекций, то следует вращать плоскость вокруг ее фронтального следа.
Если горизонтально-проецирующую плоскость вращать вокруг ее фронтального следа до совмещения с пл. π2, то горизонтальный след плоскости после Совмещения расположится на оси проекций. Также, если фронтально-проецирующую плоскость вращать вокруг ее горизонтального следа до совмещения с пл. π1 то фронтальный след плоскости расположится на оси проекций.
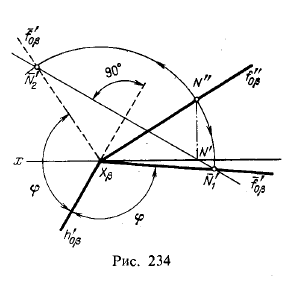
На рис. 234 изображена плоскость с тупым углом между следами f"0β и h'0β в совмещении с пл. π1 при «вращении на зрителя» и при вращении в обратном направлении.
Вопросы к §§ 36-37
- Можно ли показать на чертеже поворот, например, прямой вокруг оси, перпендикулярной к пл. π1, или пл. π2, не изображая самой оси? На чем основан такой прием?
- Какое название встречается для вращения без изображения оси?
- Как располагается плоскость вращения точки, если ось вращения последней лишь параллельна пл. π1 или пл. π2, но не перпендикулярна ни к π1 ни к π2? Почему при этом приходится определять натуральную величину радиуса вращения?
- Что служит признаком достижения горизонтального положения плоскости, заданной горизонталью и точкой, при повороте вокруг этой горизонтали и где получается фронтальная проекция точки после поворота?
- Что понимается под названием «способ совмещения»?
- Что понимается под названием «подъем в пространство»?