Способ вращения вокруг оси, перпендикулярной к плоскости проекции

Вращение вокруг оси, перпендикулярной к плоскости проекции, является частным случаем параллельного перемещения. Отличие от общего случая состоит лишь в том, что за траекторию перемещения точки берется не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между точкой и осью вращения.

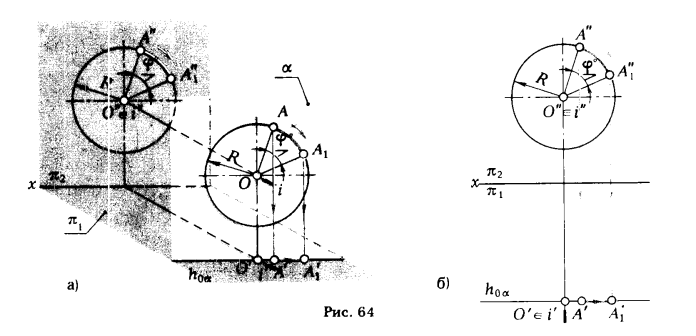
Проследим, как будет изменяться положение точки А при ее вращении вокруг оси i, перпендикулярной плоскости π₂ (рис. 64). Точка А перемещается по дуге окружности в плоскости α (α ⊥ i и, следовательно, α || π₂), поэтому эта окружность проецируется на плоскость π₂ без искажения, а на плоскость π₁ - в отрезок прямой, параллельной оси х (рис. 64,6).

Таким образом, при вращении точки вокруг оси, перпендикулярной к фронтальной плоскости проекции, фронтальная проекция точки перемещается по окружности с центром на фронтальной проекции оси вращения, а горизонтальная - по прямой, параллельной оси х.

Вращение точки вокруг оси i ⊥ π₁ иллюстрирует рис. 65,а. Точка В перемещается в новое положение В₁ по окружности, принадлежащей

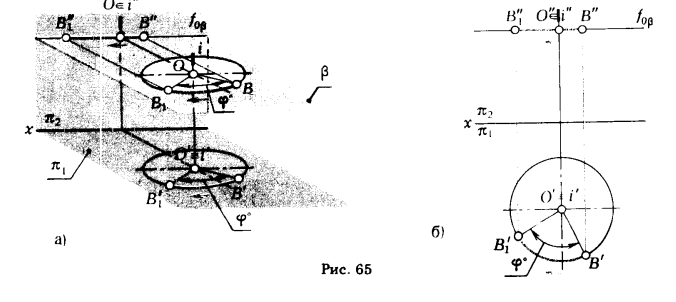
плоскости β ⊥ i. Так как i ⊥ π₁ , то β || π₁ . Поэтому при вращении точки вокруг оси, перпендикулярной к горизонтальной плоскости проекции, ее горизонтальная проекция перемещается по окружности, центр которой принадлежит горизонтальной проекции оси вращения, а фронтальная проекция точки - по прямой, параллельной оси х (рис. 65,6).

Выяснив характер проекций траекторий перемещения точки при ее вращении вокруг оси, перпендикулярной плоскости проекции, легко осуществить перемещение любой геометрической фигуры из заданного положения в частное путем ее поворота вокруг оси i ⊥ π₁ (или π₂).

В качестве примера покажем на эпюре Монжа, как осуществляется перемещение отрезка произвольной прямой в частное положение путем вращения вокруг оси, перпендикулярной плоскости проекции.

ПРИМЕР 1. [AВ] прямой общего положения а перенести в положение, параллельное π₂ (рис. 66).

Чтобы осуществить такое перемещение, достаточно повернуть [АВ] вокруг оси i ⊥ π₁ нa ∠φ° .

Величину угла 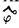выбирают такой, чтобы после поворота [A'₁B'₁] занял положение || оси х.

Так как точка В принадлежит оси вращения, то она не будет менять своего положения в процессе преобразования. B₁ ≡ В, следовательно, B'₁ ≡ В' и В"₁ ≡ В". Для нахождения точки А" необходимо из A'₁ восставить перпендикуляр к оси х и отметить точку его пересечения с горизонтальной прямей, проведенной через А".

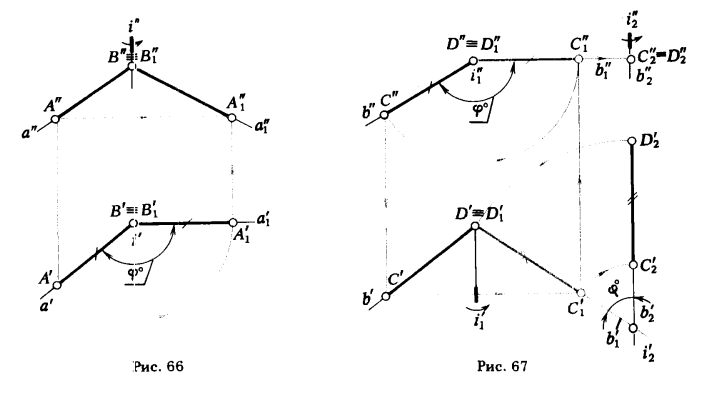
ПРИМЕР 2. [СD] прямой общего положения b перевести в положение ⊥ π₂ (рис. 67).

Чтобы осуществить перемещение отрезка из общего положения в проецирующее, необходимо последовательно выполнить два вращения вокруг осей, перпендикулярных к плоскостям проекций.

После первого вращения отрезок переводится в положение, параллельное плоскости π₁ (или π₂), и лишь после этого вращением вокруг оси, перпендикулярной плоскости проекции π₁ (или π₂) перемещают отрезок в положение, перпендикулярное плоскости π₂ (или π₁).

На рис. 67 [CD] вначале вращением вокруг i₁ ⊥ π₂ переведен в положение || π₁ ([С"₁ D"₁] || х), затем вращением вокруг i₂ ⊥ π₁ [С₁D₁] перемещен во фронтально проецирующее положение ([C'₂D'₂]⊥ x)*.

* Для упрощения геометрических построений здесь, как и во всех других случаях использования способа вращения бы она пересекала вращаемую прямую.

В случае перевода плоскости общего положения в частное задача решается аналогично только что рассмотренным примерам.

Чтобы плоскость, произвольно расположенная в пространстве, заняла проецирующее положение, достаточно вращением перевести прямую, принадлежащую этой плоскости, в положение, перпендикулярное плоскости проекции .Количество графических построений, которые необходимо выполнить для такого перемещения, может быть сокращено, если взять не произвольную прямую, а горизонталь или фронталь плоскости. Уменьшение графических построений в этом случае происходит благодаря тому, что перевод горизонтали или фронтали в проецирующее положение можно осуществить за один поворот, а не за два, как это пришлось бы делать, если поворачивать прямую общего положения.

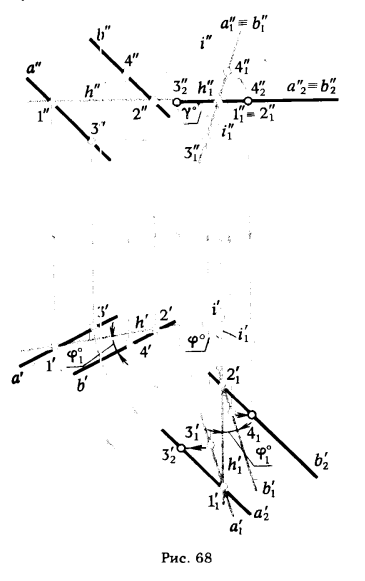
На рис. 68 плоскость общего положения α, заданная параллельными прямыми а и b, поворотом вокруг оси i ⊥ π₁ переведена во фронтально проецирующее положение. Новые проекции прямых а₁ и b₁ найдены с помощью горизонтали h.

Геометрические построения, приведенные на рис. 68, выполняем в следующем порядке:

1. В плоскости α проводим горизонталь h (h' , h" ) .

2. Вращением вокруг оси i, проходящей через горизонталь h и перпендикулярную плоскости π₁ , переводим h (h' , h") в положение h₁ (h'₁, h"₁)⊥ π₂.

3. При повороте горизонтали на ∠ φ° на такой же угол повернется все множество точек этой плоскости, поэтому для определения нового положения проекций прямых а₁ и b₁ достаточно повернуть вокруг оси i точки 1, 3 и 2, 4 (3 ∈ а, 4 ∈ b) на тот же ∠ φ° .

По горизонтальным проекциям 1'₁, 3'₁ и 2'₁, 4'₁ определяем их фронтальные проекции.

Если необходимо перевести плоскость в положение || π₁, то это легко сделать, повернув фронтальные проекции прямых а"₁ и b"₁ вокруг оси i₁ ⊥ π₂ на угол γ° так, чтобы а"₂ и b"₂ заняли положение, параллельное оси х.

* Новое положение а'₁ и b'₁ можно определить и иначе: через 1'₁ и 2'₁, провести прямые а'₁ и b'₁, составляющие с прямой h'₁ такой же угол, какой а' и b' составляют с h'.