Замена одной плоскости проекции
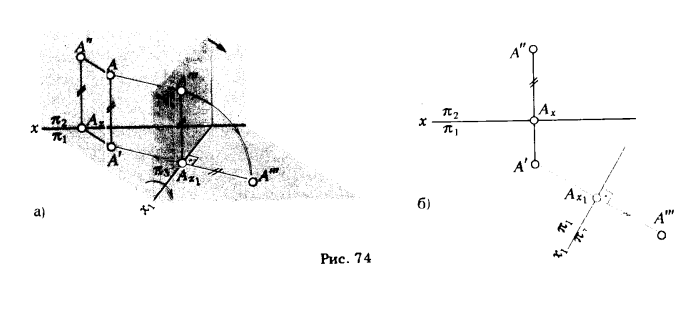
ТеорияПусть в системе плоскостей х·π2/π1 дана точка А и указаны ее проекции А' и А" (рис. 74,а). Проследим, как изменится положение проекций точки А, если плоскость π2 заменить новой плоскостью π3, перпендикулярной к π1 . Горизонтальная плоскость проекции не меняет
* Следует иметь в виду, что В. Л. Тороховым предложен способ замены плоскостей π1 и π2 одновременно двумя взаимно перпендикулярными плоскостями π3 и π4, что позволяет осуществить непосредственный переход от х· π2/π1 к х2·π3/π4, минуя промежуточное звено x1·π3/π1 или x1·π2/π3 . Подробно с этим способом можно познакомиться в книге С. А. Фролова "Методы преобразования ортогональных проекций". М.: Машиностроение, 1970.
своего положения, т. е. мы осуществляем переход от Системы х · π2/π1 к новой системе x1· π3/π1 . Плоскость π3 пересекается с плоскостью π1 по прямой х1, которая определяет новую ось проекции. Положение горизонтальной проекции А' точки А остается без изменения, так как точка А и плоскость π1 не меняли своего положения в пространстве.
Для нахождения новой фронтальной проекции точки А'" достаточно спроецировать ортогонально точку А на плоскость π3. Из чертежа видно, что расстояние от новой фронтальной проекции А'" точки А до новой оси x1 равно расстоянию от старой фронтальной проекции A" до старой оси х (|A'"Ax 1| = |А"Аx|).
Чтобы перейти от пространственного макета к эпюру, необходимо совместить плоскость π3 с плоскостью чертежа. Метод замены плоскостей проекций предусматривает совмещение новой плоскости с той из старых плоскостей, к которой она перпендикулярна. В рассматриваемом случае ввиду перпендикулярности плоскостей π3 и π1 плоскость π3 совмещена с π1. За ось вращения принята новая ось проекций x1. Направление поворота не оказывает никакого влияния на результат преобразования. Поворот следует делать в таком направлении, при котором новые проекции не накладываются на старые и не затрудняют чтения чертежа. На рис. 74,а совмещение плоскости π3 с π1 осуществлено вращением ее по направлению движения часовой стрелки.
Равенство аппликат новой А'" и старой А" фронтальных проекций точки А и использование в обоих случаях прямоугольного проецирования делают построение новой фронтальной проекции чрезвычайно простым. Оно состоит в том, что через старую горизонтальную проекцию точки проводят прямую, перпендикулярную к новой оси, и откладывают на ней от точки пересечения с осью отрезок, равный расстоянию от старой фронтальной проекции до старой оси (рис. 74,6).
Замена горизонтальной плоскости π1 новой плоскостью π3 и построение новых проекции точки А в системе x1·π2/π3 осуществляется аналогично только что рассмотренному случаю, с той лишь разницей, что теперь оггается без изменения фронтальная проекция точки, а для нахождения новой горизонтальной проекции А'" точки А необходимо из старой фронтальной проекции точки опустить перпендикуляр на новую ось х1 и отложить на нем от точки пересечения с осью х1 отрезок, равный расстоянию от старой горизонтальной проекции до старой оси х.
Построения, выполненные по этому правилу, приведены на рис. 75. На рис. 76 показан отрезок [АВ], произвольно расположенный в про-
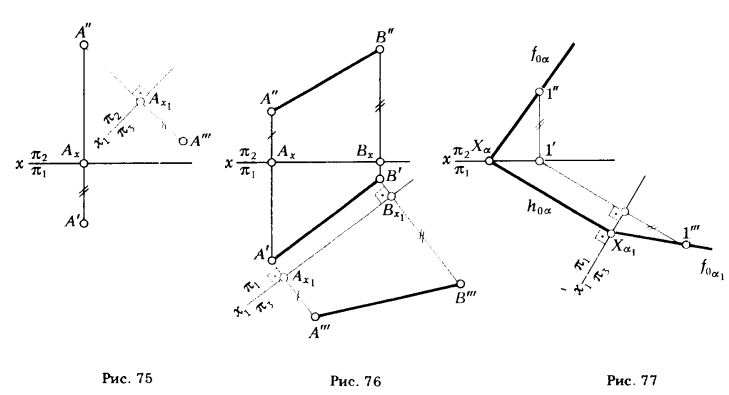
странстве, и его новая фронтальная проекция на плоскость π3, которой он параллелен. Все построения ясны из чертежа и не требуют пояснения.
На рис. 77 приведено решение задачи, при котором плоскость общего положения а оказалась фронтально проецирующей относительно плоскости π3. Известно, что горизонтальный след фронтально проецирующей плоскости перпендикулярен к оси х, следовательно, чтобы плоскость α заняла фронтально проецирующее положение, необходимо новую ось x1 провести перпендикулярно к h0α. Через точку Xα1, в которой h0α ∩ x1 , пройдет фронтальный след f0 α1. Для определения его направления достаточно найти одну точку. В качестве такой точки можно взять произвольную точку 1" ∈ f0α и указать ее фронтальную проекцию 1'" на новой плоскости π3. Через Xα1 и 1"' проводим f0 α1 .