Ортогональные проекции поверхности

Вы уже знаете, что две ортогональные проекции на две непараллельные плоскости однозначно определяют положение точки и положение и вид линии. Переходя к рассмотрению ортогональных проек-

* R_i — преобразование (рассматривается как вращение вокруг оси i) , переводящее любые точки А и В в такие точки А₁ и B_i, что |АВ| = |А₁ В₁|.

** Т_i — преобразование (рассматривается как параллельное перемещение), переводящее точки A и В в такие точки А₁ и B_i, что |АВ| = |А₁ В₁|.

ций поверхностей, мы обнаруживаем, что некоторые поверхности не могут быть заданы своими проекциями. В справедливости этого утверждения можно убедиться на примере проецирования простейшей поверхности — плоскости. Действительно, если мы будем проецировать все точки плоскости, занимающей произвольное положение по отношению к плоскостям проекций, то проекции множества точек плоскости покроют полностью все плоскости проекций. Это произойдет потому, что плоскость является незамкнутой поверхностью — она может быть безгранично продлена в любом направлении.

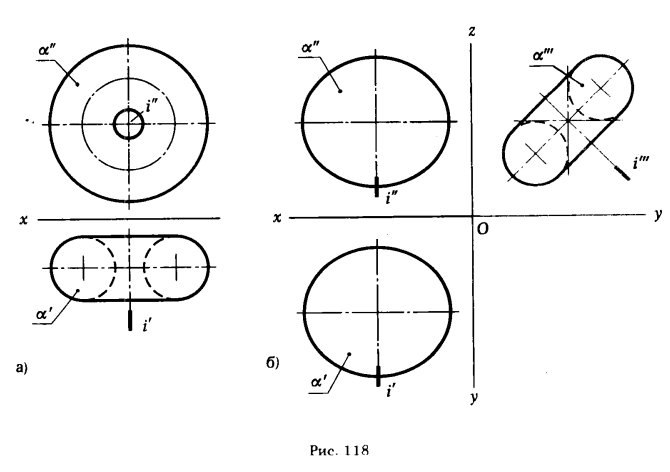
Не только незамкнутые поверхности невозможно задать проекциями всех принадлежащих им точек, но и ряд замкнутых поверхностей при определенной ориентации их к плоскостям проекций не могут быть определены (заданы) ортогональными проекциями их точек, например, если ось поверхности кольца занимает положение, перпендикулярное к плоскости проекции, то кольцевую поверхность можно задать ее двумя ортогональными проекциями (рис. 118,а), но стоит только перевести ось кольца в наклонное положение, как задание этой поверхности двумя ортогональными проекциями (на те же плоскости проекций) становится невозможным (рис. 118,6).

Чтобы задать поверхность на чертеже, достаточно указать проекции не всего множества точек или линий, принадлежащих поверхности, а только некоторых из них, с помощью которых может быть установлено взаимно однозначное соответствие между образом (проекцией) и прообразом (объектом проецирования). Такими точками или линиями могут быть точки или линии, входящие либо в состав определителя поверхности, либо в ее каркас (точечный или линейный). В первом случае поверхность задается определителем, во втором — каркасом.

Задание поверхности проекциями ее определителя не всегда обеспечивает наглядность, а это, в свою очередь, затрудняет чтение чертежа, поэтому для получения наглядного изображения поверхности на эпюре

Монжа в ряде случаев следует указывать очерк (очертание) этой поверхности.

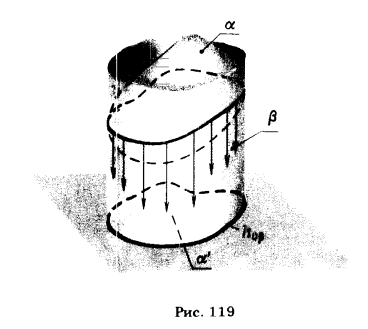
Очерком поверхности (при ортогональном проецировании) называют след на плоскости проекции проецирующей цилиндрической поверхности, которая огибает заданную поверхность.

Рис. 119 дает наглядное представление о том, как получается очерк произвольной замкнутой поверхности α на горизонтальную плоскость проекции.