Нелинейчатые поверхности с образующей переменного вида

Эта группа поверхностей имеет единый по форме определитель

Ф (g̃₁, ... ,g̃_n;ᵭ₁,ᵭ₂,ᵭ₃); [ {̃g₁, ... ,̃g_n } ∩ { ᵭ₁, ᵭ₂, ᵭ₃ } ≠ ∅]*,

в котором g̃_j - образующая переменного вида, d₁; d₂, d₃ - направляющие *.

Примечание. В ряде случаев закон перемещения образующей может быть задан не тремя, а двумя (ᵭ₁, ᵭ₂ ) и даже одной (ᵭ₁ ) направляющей. В двух последних случаях вместо отсутствующих направляющих указываются дополнительные условия.

В качестве примера можно привести поверхность α, показанную на рис. 115, у которой закон перемещения образующей g_j направляющими ᵭ₁ и ᵭ₂ и плоскостью у, которая выполняет функции третьей направляющей d3. Определитель этой поверхности имеет вид

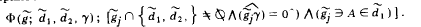
* Здесь, как и в определителе поверхностей групп Б_I А_II, Б_II (см. § 28, 30, 32, 33, 34), некоторые из направляющих d₁, d₂, d₃ могут быть не только кривыми ᵭ, но и прямыми d линиями.

Таблица 2. Нелинейчатые поверхности с образующей переменного вида. Группа А_I; Ф (g̃₁,..., g̃_n; ᵭ₁, ᵭ₂, ᵭ₃); [{̃₁,..., g̃_n} ∩ {ᵭ₁, ᵭ₂, ᵭ₃} ≠ ∅ ]

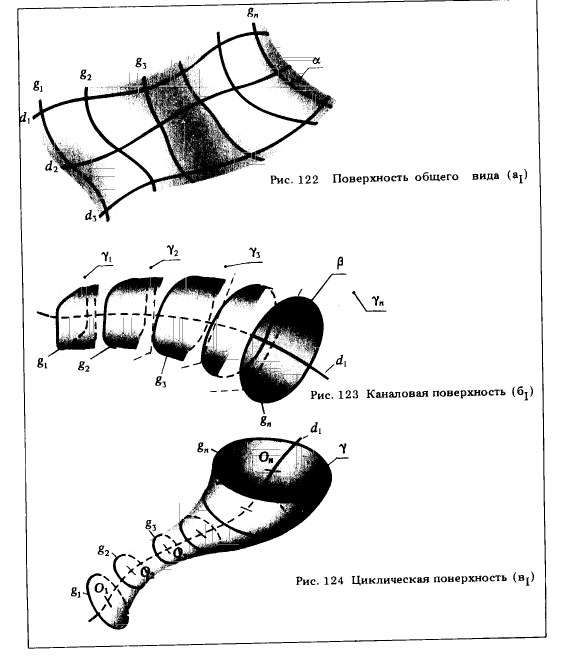
Смысловое значение алгоритмической части этого определителя может быть выражено следующим предложением: криволинейная образующая (g̃) пересекает направляющие ᵭ₁ и ᵭ₂ (пересечение g̃_j с ᵭ₁ и ᵭ₂ является не пустым множеством - g̃_j ∩ { ᵭ₁, ᵭ₂} ≠ ∅) и образующая g̃_jпараллельна плоскости 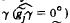, а точка А, принадлежащая образующей g̃_j, скользит по направляющей ᵭ₁ (g̃_j ∋ А ∈ ᵭ₁).

Другим примером может служить трубчатая поверхность β (см. рис. 126), у которой задана только одна направляющая ᵭ₁. Отсутствие направляющих ᵭ₂ и ᵭ₃ компен-

сируется дополнительным условием, входящим в алгоритмическую часть определителя этой поверхности, которое заключается в том, что центр окружности О перемещается вдоль направляющей ᵭ₁ , а ее плоскость γ все время остается перпендикулярной к ᵭ₁.

Рассматриваемая группа поверхностей включает в себя три подгруппы.

1. Подгруппа a_I - поверхность общего вида α (табл. 2, рис. 122). Такая поверхность может быть образована перемещением произвольна (плоской или пространственной) кривой g̃_j по направляющим ᵭ₁, ᵭ₂, ᵭ₃. В процессе движения образующая g̃_j все время меняет свою форму, принимая вид g̃₁,g̃₂,g̃₃, ... , g̃_n;

Подгруппа б_I - каналовая поверхность β (табл. 2, рис. 123). Каналовой поверхностью называют поверхность, образованную непрерывным каркасом замкнутых плоских сечений, определенным образом ориентированных в пространстве. Площади этих сечений могут оставаться постоянными или монотонно изменяться в процессе перехода от одного сечения к другому. В инженерной практике наибольшее распространение получили два способа ориентирования плоскостей образующих:

1) параллельно какой-либо плоскости - каналовые поверхности с плоскостью параллелизма;

2) перпендикулярно к направляющей линии - прямые каналовые поверхности.

Каналовая поверхность может быть использована для создания переходных участков между двумя поверхностями типа трубопроводов, имеющих:

а) различную форму, но одинаковую площадь нормального сечения;

б) одинаковую форму, но различные площади сечения;

в) различную форму и различные площади поперечных сечений.

3. Подгруппа в_I - циклическая поверхность γ (табл. 2, рис. 124). Циклическую поверхность можно рассматривать как частный случай каналовой поверхности. Она образуется с помощью окружности, центр которой перемещается по криволинейной направляющей. В процессе движения радиус окружности монотонно меняется.