Линейчатые поверхности

^Теория

Линейчатая поверхность в общем случае однозначно определяется тремя направляющими линиями. Действительно, пусть даны три пространственные кривые линии ᵭ₁, ᵭ₂ и ᵭ₃(рис. 127). Возьмем на кривой ᵭ₁ произвольную точку М, примем ее за вершину конической поверхности α, а за направляющую этой поверхности примем дугу кривой ᵭ₃. Если N - точка пересечения дуги кривой ᵭ₂ с поверхностью α, то (MN) пересечет дугу кривой ᵭ₃ в точке L. То, что (MN) обязательно пересечет дугу кривой d₃, не вызывает сомнения, так как (MN) и кривая d₃ принадлежит одной и той же поверхности α. Из рис. 127 видно, что через точку М, взятую на направляющей ᵭ₁, проходит одна прямолинейная образующая g, пересекающая две другие направляющие ᵭ₂ и ᵭ₃*. Задавая другое положение точки М → М₁ и принимая точку М₁ за вершину конической поверхности, мы получим при той же направляющей ᵭ₃ отсек новой конической поверхности α₁, которую дуга кривой ᵭ₂ пересечет в точке N₁ . Точки М₁ и N₁ определяют прямую (M₁N₁ ), которая пересечет третью направляющую ᵭ₃ в точке L₁. (М₁L₁) - новая образующая g₁ линейчатой поверхности.

Описанным способом можно построить любое число прямолинейных образующих, которые выделят в пространстве одну единственную линейчатую поверхность. Следует иметь в виду, что нельзя за направляющие брать три различные по форме и произвольно расположенные линии. Произвольно можно задавать только две направляющие, форму и положение третьей направляющей выбирают так, чтобы она находилась внутри конгруенции** прямых, определяемой двумя уже взятыми направляющими.

Чтобы третья направляющая принадлежала линейчатой поверхности, она должна входить внутрь конгруенции, определяемой первыми двумя направляющими. Иными словами, задав дуги двух направляющих линей-

* Несмотря на то, что кривые ᵭ₁, ᵭ₂ и ᵭ₃, показанные на рис. 127, будут кратными (через точку М проходит не одна, а n₂ × n₃ образующих, где n₂ - порядок кривой ᵭ₂, n₃ - порядок кривой ᵭ₃ ), мы рассматриваем случай, когда, линия d₁ пересекает коническую поверхность α, заданную точкой М и направляющей ᵭ₃, только один раз. Такое допущение возможно в том случае, если рассматривать не всю поверхность α, а только ее отсек, в формировании которого принимает участие не вся кривая ᵭ₃, а только ее дуга 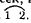Формула .

** Под конгруенцией прямых подразумевается множество прямых, зависящих от двух параметров. Например, если взять две произвольные кривые ᵭ₁ и ᵭ₂ (рис. 128) и на кривой ᵭ₁, отметить точку М, приняв ее за вершину конической поверхности с направляющей ᵭ₂, то мы получим множество прямых (образующих конической поверхности), проходящих через точку М ∈ d₁, и одну из точек, принадлежащих множеству, определяющему линию ᵭ₂. Если принять, что точка М будет перемещаться по кривой ᵭ₁, последовательно занимая положения M₁, М₂, М₃,..., М_n, то мы получим новые конические поверхности α₁, α₂, α₃, ... , α_n, прямолинейные образующие которых заполнят некоторый отсек пространства. Множество всех прямых - образующих конических поверхностей, за вершины которых взяты последовательно все точки одной линии ᵭ₁(ᵭ₂ ), а за направляющую принята вторая линия ᵭ₂ (ᵭ₁), является двупараметрическим множеством, т. е. конгруенцией.

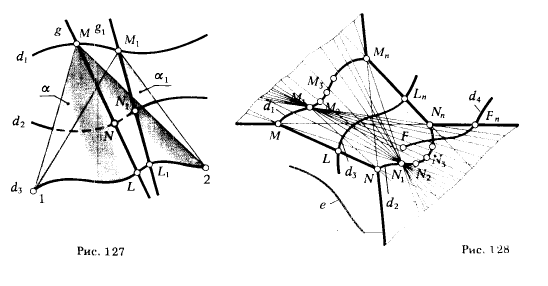
чатой поверхности, мы определяем область ее существования. На рис. 128 эта область ограничена линиями красного цвета. Очевидно, дуга кривой ᵭ₃, ограниченная точками L и L_n будет принимать участие совместно с дугами кривых 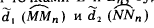Формула в образовании линейчатой поверхности ( 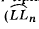лежит внутри конгруенции). Кривая ᵭ₄ может быть использована в качестве третьей направляющей только на участке 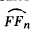(т. е. в той части, которая лежит внутри конгруенции).

Кривая е, не погруженная в область конгруенции прямых, не будет принадлежать линейчатой поверхности и, следовательно, не может быть принята за третью направляющую*.

Теперь, после того как мы познакомились с требованием к заданию третьей направляющей линейчатой поверхности, можно перейти к рассмотрению различных групп этих поверхностей и, в частности, рассмотреть задание их на чертеже, а также возможности использования в технике.