Линейчатые поверхности с двумя направляющими

Движение прямой - образующей по трем направляющим, не единственный способ образования линейчатой поверхности. Только что доказанная теорема убедительно подтверждает справедливость такого высказывания. Из этой теоремы вытекает важное следствие: линейчатая поверхность может быть однозначно определена двумя направляющими и плоскостью параллелизма.

В этом случае определитель линейчатой поверхности примет вид

Ф(g; ᵭ₁, ᵭ₂, γ); [g_j ∩ { ᵭ₁, ᵭ₂,}≠ ∅ ∧ (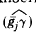) = φ°)] .

Здесь γ - направляющая плоскость. В частном случае, если угол между 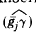= 0° (образующая параллельна плоскости γ), то γ называют плоскостью параллелизма.

Пусть будут заданы две произвольные кривые d₁ и d₂ и плоскость γ. Можно задать такой закон перемещения прмолинейной образующей g_j, при котором она, скользя по линиям d₁ и d₂, все время сохраняет постоянный ∠φ° с плоскостью γ. Плоскость γ заменяет ту третью направляющую, которая образуется множеством точек пересечения движущейся прямолинейной образующей g_j с плоскостью γ.

В рассматриваемую группу поверхностей входят три подгруппы: а) цилиндроиды, б) коноиды, в) косые плоскости.

Перечисленные подгруппы поверхностей могут быть отнесены к двум разновидностям:

поверхности, образованные с помощью направляющей плоскости;

поверхности, в создании которых принимала участие плоскость параллелизма.

К первой разновидности относятся косые линейчатые поверхности (косой цилиндроид, косой коноид, дважды косая плоскость); ко второй - прямые линейчатые поверхности (прямой цилиндроид, прямой коноид, косая плоскость). Поверхности с плоскостью параллелизма называются поверхностями Каталана*. Из линейчатых поверхностей с двумя направляющими рассмотрим только поверхности Каталана, так как именно эти поверхности находят широкое применение в технике.