Линейчатые поверхности с одной направляющей - торсы
ТеорияРассматриваемая в этом параграфе группа линейчатых поверхностей с одной криволинейной направляющей называется торсами, а криволинейная направляющая таких поверхностей - ребром возврата *.
Поверхностью с ребром возврата (торсом) называют поверхность, описываемую движением прямой - образующей g, касающейся некоторой пространственной кривой - направляющей ᵭ.
Торсы обладают замечательным свойством - они могут быть совмещены с плоскостью без складок и разрывов, путем последовательных ее изгибов по прямолинейным образующим. В связи с этим можно дать и другое определение поверхности торса. Торсом называют линейчатую поверхность, которую можно совместить всеми ее точками с плоскостью без складок и разрывов. Такие поверхности называют также развертывающимися поверхностями.
Если ребро возврата вырождается в точку, то получается частный вид торса - коническая поверхность (если точка собственная) или цилиндрическая поверхность в случае вырождения ребра возврата в несобственную точку.
Итак, к рассматриваемой группе линейчатых поверхностей относятся:
1) поверхность с ребром возврата (табл. 6, рис. 146);
2) поверхность коническая (табл. 6, рис. 147) ;
3) поверхность цилиндрическая (табл. 6, рис. 148).
В частном случае торсовые поверхности преобразуются в плоскость. Для этого достаточно, чтобы ребро возврата ᵭ1 преобразовалось в плоскую кривую, а направляющая d1 конической или цилиндрической поверхности - в прямую линию. Определитель этой группы поверхностей имеет вид
Ф(g, ᵭ1,S); [gj  ᵭ1 = Sj ∈ ᵭ1) ].
ᵭ1 = Sj ∈ ᵭ1) ].
Рассмотрим более подробно каждую из отмеченных поверхностей.
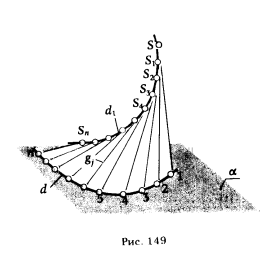
1. Поверхность с ребром возврата. Образование этой поверхности можно представить таким образом. Пусть даны плавная кривая d и точка S, причем S ∈ α ⊃ d (рис. 149). Разделим кривую d на n участков, границы которых отметим точками 1, 2, 3, ... , n. Проведем прямую S1 и отложим на ней от точки S вниз [SS1]. Конец отрезка S1 соединим прямой с точкой 2 ∈ d, получим отсек конической поверхности S1 1 2.
* Ребро возврата следует рассматривать как кривую, в которой "совпадают" все три криволинейные направляющие линейчатой поверхности d1 ≡ d2 ≡ d3.
Таблица 6. Линейчатые поверхности одной направляющей - торсы. Группа ВII; Ф(g, ᵭ1,S); [gj  ᵭ1 = Sj ∈ ᵭ1) ]
ᵭ1 = Sj ∈ ᵭ1) ]
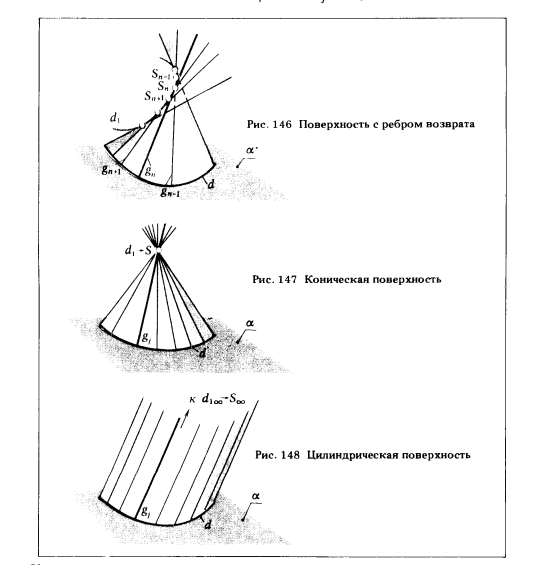
На прямой (S1 2) откладываем [S1S2] и конец отрезка S2 соединяем с точкой 3 ∈ d - вновь получаем отсек конической поверхности S223. Повторяя описанные операции n раз, мы получим n следующих один за другим отсеков конических поверхностей с вершинами в точках S1, S2, S3, ... , Sn. Если уменьшить длину отрезков [SS1 ], [S1S2], [S2S3], ... , [Sn-1Sn], то ломаная линия SS1S2S3 ... Sn в пределе превратится в плавную пространственную кривую d1 , называемую ребром возврата, а прямолинейные звенья этой ломаной линии перейдут в касательные к кривой d1. Непрерывное множество этих касательных образует поверхность с ребром возврата (торс).
Из рис. 146 видно, что поверхность с ребром возврата имеет две полы. Ребро возврата служит границей этих пол. Так как в каждой точке плавной кривой можно провести только одну касательную, то
при задании поверхности с ребром возврата направляющую - кривую d можно не указывать. Поэтому определитель такой поверхности будет иметь вид
Ф(g, ᵭ1,S); [gj  ᵭ1 = Sj ∈ ᵭ1) ]
ᵭ1 = Sj ∈ ᵭ1) ]
где ᵭ1 - пространственная плавная кривая - ребро возврата, g - прямая образующая, S - точка, принадлежащая кривой ᵭ1 . Условие, отражающее закон движения прямолинейной образующей, состоит в том, что она, двигаясь вдоль ребра возврата, все время остается касательной к нему.
В машиностроении находит применение частный вид торсовой поверхности, у которой ребром возврата служит цилиндрическая винтовая линия. Полученную с помощью этой линии поверхность называют винтовым торсом. На рис. 150 показаны ортогональные проекции отсека поверхности винтового торса.
2. Коническая поверхность. Все прямолинейные образующие конической поверхности пересекаются в собственной точке S. Это условие соблюдается лишь в том случае, когда ребро возврата ᵭ1 вырождается в собственную точку S (см. рис. 147). Определитель конической поверхности имеет вид
Ф(g, ᵭ1,S); [gj ∩ ᵭ1≠ ∅ ∧ ∩gj = S ]
Приведенная символическая запись определителя конической поверхности показывает, что эта поверхность однозначно определяется прямолинейной образующей, кривой направляющей и точкой S, при этом прямолинейная образующая пересекает направляющую (gj ∩ ᵭ ≠ ∅ - пересечение gj и ᵭ не пустое множество) и все образующие пересекаются в одной точке ( ∩ gj = S).
На рис. 151 показано задание конической поверхности на эпюре Монжа. Проекции образующих g1, g2, g3, ... , gn на рис. 151 указаны только для наглядности. Коническая поверхность однозначно задается проекциями ее образующей, направляющей и вершиной (gjd, S).
3. Цилиндрическая поверхность получается в том случае, когда все прямолинейные образующие пересекаются в несобственной точке S∞.
В этом случае определитель поверхности может быть записан:
Ф(g, ᵭ,S∞); [gj ∩ ᵭ ≠ ∅ ∧ ∩ gj = S∞ ]
Отличие определителя цилиндрической поверхности от определителя конической поверхности состоит лишь в том, что образующие цилиндрической поверхности параллельны (пересекаются в несобственной точке), в то время как для конической поверхности характерным является пересечение всех ее прямолинейных образующих в собственной точке.
На рис. 148 (табл. 6) показана произвольная цилиндрическая поверхность. Рис. 152 дает представление о ее задании на эпюре Монжа.
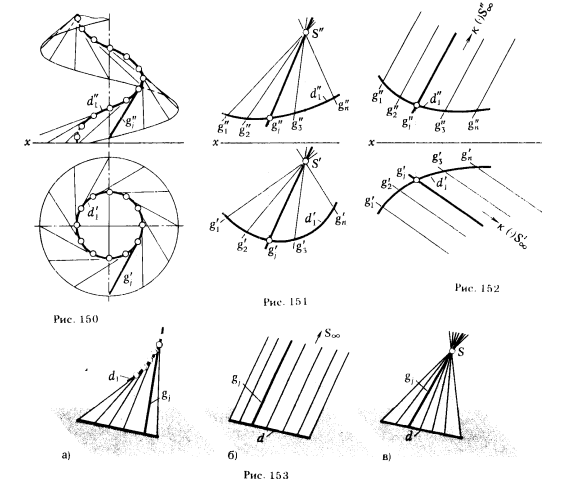
4. Плоскость. Раньше было отмечено, что частным случаем торсовых поверхностей является плоскость, и указаны условия, при которых поверхность с ребром возврата, коническая и цилиндрическая преобразуются в плоскость. Рис. 153 дает наглядное представление об этих преобразованиях.