Общий способ построения линии пересечения одной поверхности другою

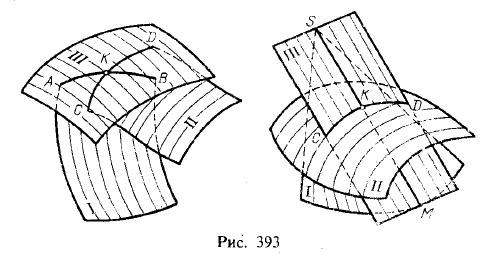
Общим способом построения линии пересечения одной поверхности другою является нахождение точек этой линии при помощи некоторых секущих поверхностей ¹). На рис. 393 слева показано, что поверхности I u II пересечены некоторой поверхностью III; эта вспомогательная поверхность пересекает поверхность I по линии АВ, а поверхность II — по линии CD. Точка К, в которой пересекаются линии АВ и CD, общая для поверхностей I и II, следовательно, принадлежит линии их пересечения. Повторяя такой прием, получаем ряд точек искомой линии. Мы уже пользовались этим способом, когда рассматривали (см. § 24) построение линии

пересечения одной плоскости другою плоскостью. Тогда дело сводилось (рис. 166) к использованию двух вспомогательных плоскостей. Каждая из них позволяла найти одну точку, общую для плоскостей, линию пересечения которых надо было найти.

Применяя указанный общий способ для построения линии пересечения двух кривых поверхностей, мы можем:

1) пересекать поверхности вспомогательными плоскостями;

2) пересекать поверхности вспомогательными кривыми поверхностями (например, сферами).

В некоторых случаях при решении задач комбинируют применение вспомогательных плоскостей и кривых поверхностей. Следует по возможности подбирать такие вспомогательные поверхности, которые в пересечении с данными поверхностями дают простые для построения линии (например, прямые или окружности).

¹) Для линий пересечения применяется также название «линии перехода», особенно в тех случаях, когда при переходе от одной поверхности к другой нет ярко выраженного пересечения. Для вспомогательных секущих поверхностей встречается название «посредники».

В общем случае вспомогательные секущие плоскости применяют и для построения линии пересечения кривой поверхности гранной.

Изложенный общий способ построения линии пересечения одной поверхности другою не исключает применения другого способа, если хотя бы одна из этих поверхностей линейчатая: найти точку, в которой прямолинейная образующая одной поверхности пересекает другую поверхность, и, повторяя этот прием для ряда образующих, через найденные точки провести искомую линию. На рис. 393 справа показано, что через образующую SM поверхности I проведена плоскость III, которая пересекает вторую поверхность (II) по кривой CD; образующая SM пересекает эту кривую в точке К, через которую пройдет искомая линия пересечения поверхностей I и II.

Это относится и к случаю пересечения кривой поверхности гранной: здесь роль образующих играют ребра гранной поверхности.

Итак, для построения точек линии, получающейся на одной поверхности при пересечении ее другой поверхностью, пользуются вспомогательными секущими плоскостями частного и общего положения, кривыми поверхностями, прямолинейными образующими кривых линейчатых поверхностей и ребрами гранных поверхностей. При этом прибегают к способам преобразования чертежа, если это упрощает и уточняет построения.

В примерах, приведенных в последующем изложении, преимущественно рассмотрены геометрические тела, т. е. ограниченные части пространства вместе с их границами — поверхностями. Из двух поверхностей только одна пересекает другую. Поэтому одна из поверхностей сохраняется, а на другой, пересекаемой, возникают отверстия. Здесь может быть: 1) проницание, причем получаются или две отдельные линии (см., например, рис. 412, где конус с горизонтальной осью входит в другой конус), или одна линия с узловой точкой (рис. 427); 2) врезка, когда получается одна линия (см., например, рис. 396, 426).

На литых деталях обычно бывают плавные переходы, т. е. переход от одной поверхности к другой по некоторой промежуточной, например тору. Тогда для обозначения перехода строится линия пересечения геометрических форм, лежащих в основе форм технических (см., например, рис. 399, 430)¹).

Проекции линии пересечения получаются в пределах общей части проекций обеих поверхностей.

При построении точек линии пересечения сначала следует найти те точки, которые обычно называют характерными ²). Это точки, проекции которых отделяют видимую часть проекции линии пересечения от невидимой, это. проекции точек линии пересечения, наивысших и наинизших по отношению к пл. π₁ ближайших и наиболее удаленных по отношению к зрителю, крайних слева и справа на проекциях линии пересечения.