Метрические задачи

В § 6 гл. I отмечалось, что при параллельном, в частности ортогональном, проецировании геометрические фигуры, произвольно расположенные по отношению к плоскостям проекций, проецируются на эти плоскости с искажением их метрических характеристик (характеристик, которые могут быть получены путем измерения линейных и угловых величин). Для того чтобы иметь возможность по метрически искаженным проекциям судить о размерах и форме оригинала, необходимо знать способы решения задач по определению неискаженных линейных и угловых величин.

Метрическими называются задачи, решение которых связано с нахождением характеристик геометрических фигур, определяемых (измеряемых) линейными и угловыми величинами.

Все многообразие метрических задач, в конечном счете, сводится к двум видам: А - задачам на определение расстояния между двумя точками; Б - задачам на нахождение величины угла между двумя пересекающимися прямыми.

К метрическим относятся также задачи на построение отрезка и угла с наперед заданным значением соответственно линейной и градусной (радианной) величины.

Несмотря на то, что чисто метрические задачи встречаются редко, целесообразно выделйть их в самостоятельную группу, включив в нее и те задачи, в которых на промежуточных этапах решения приходится выяснять позиционные отношения между геометрическими фигурами.

В основе алгоритма решения любой метрической задачи лежит инвариантное свойство ортогонального проецирования, заключающееся в том, что любая фигура, принадлежащая плоскости, параллельной плоскости проекции, проецируется на эту плоскость в конгруентную фигуру, т. е. (Ф ⊂ β) ∧ (β || π₁) ⇒ Ф' ≅ Ф.

Рассмотрим возможные пути решения задач на определение метрических характеристик геометрических фигур.

А. Определение расстояний.

Решение задач на определение расстояния между точкой и прямой, двумя параллельными прямыми, точкой и плоскостью, прямой и плоскостью, двумя плоскостями, скрещивающимися прямыми, в конечном счете, сводится к нахождению расстояния между двумя точками.

Чертежи на рис. 248 подтверждают это утверждение. Из этих чертежей видно также, что, прежде чем приступить к решению задачи на определение расстояния между точкой и прямой или двумя параллельными прямыми (рис. 248,а и б), необходимо провести плоскость γ, перпендикулярную к прямой l, или опустить перпендикуляр из точки А (A ∈ m или A ∈ β) на плоскость α (рис. 248, в, г, д, е). Поэтому, прежде чем решать задачи на определение расстояний, выясним характер и последо-

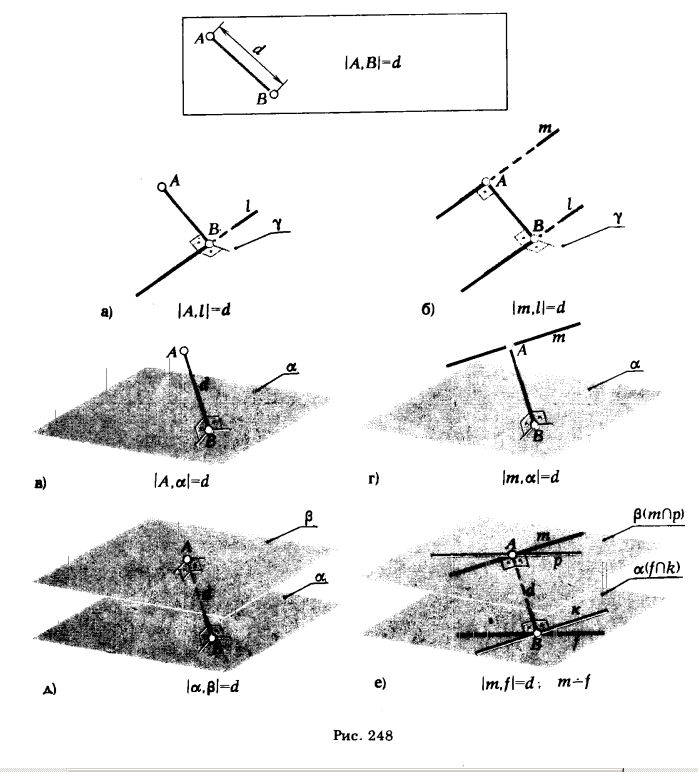
вательность графических построений, которые должны быть выполнены для построения на эпюре взаимно перпендикулярных прямых, прямой и плоскости, плоскостей.

• Построение взаимно перпендикулярных прямых, прямой и плоскости, плоскостей

  Не будет преувеличением утверждать, что построение взаимно перпендикулярных прямых и плоскостей наряду с определением расстояния между двумя точками являются основными графическими операциями при решении метрических задач.Подробнее

• Определение расстояния между двумя точками

  В § 8 гл. I (см. рис. 50) было показано графическое определение длины отрезка [АВ], являющегося мерой расстояния между точками А и В, путем построения прямоугольного треугольника.Подробнее

• Определение расстояния между точкой и прямой, между параллельными прямыми

  Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую.Подробнее

• Определение расстояния между точкой и плоскостью, прямой и плоскостью, между плоскостями и скрещивающимися прямыми

  Определение расстояния между: 1 - точкой и плоскостью; 2 - прямой и плоскостью; 3 - плоскостями; 4 - скрещивающимися прямыми рассматривается совместно, так как алгоритм решения для всех этих задач по существу одинаков и состоит из геометрических построений, которые нужно выполнить для определения расстояния между заданными точкой А и плоскостью α.Подробнее

• О проекциях плоских углов

  Отметим ряд свойств ортогональных проекций плоских углов, знание которых поможет в дальнейшем правильно читать эпюр и решать задачи по определению величины угла, если известны его ортогональные проекции.Подробнее

• Определение величины плоского угла по его ортогональным проекциям

  В предыдущем параграфе было отмечено, что плоский угол проецируется на плоскость проекции без искажения в том случае, когда его стороны параллельны этой плоскости. Это свойство может быть принято за основу при составлении алгоритма решения задачи на определение величины угла по его искаженным ортогональным проекциям.Подробнее

• Определение угла между прямой и плоскостью

  Определение угла между прямой и плоскостью, двумя плоскостями, скрещивающимися прямыми, сводится к нахождению угла между двумя прямыми.Подробнее

• Определение угла между плоскостями

  Мерой угла между двумя плоскостями служит линейный угол, образованный двумя прямыми - сечениями граней этого угла плоскостью, перпендикулярной к их ребру.Подробнее

• Определение угла между скрещивающимися прямыми

  Углом между скрещивающимися прямыми называется плоский угол, который образуется между прямыми, проведенными из произвольной точки пространства параллельно данным скрещивающимся прямым.Подробнее