Способы преобразования ортогональных проекций, перемены плоскостей проекций и вращения
ТеорияПонятая и определения
Трудоемкость и, как следствие, точность графического решения задач часто зависят не только от сложности задач, но и от того, какое положение занимают геометрические фигуры, входящие в условия задачи, по отношению к плоскостям проекций.
Проиллюстрируем сказанное примерами.
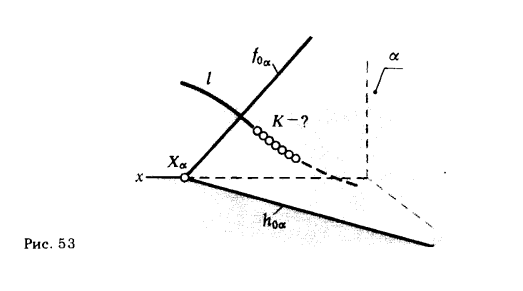
ПРИМЕР 1. Требуется определить точку пересечения ("встречи") линии l с плоскостью α (рис. 53).
Так как и линия l, и плоскость α занимают произвольное положение как по отношению друг к другу, так и относительно плоскостей проекций, то ответить на поставленный вопрос непосредственно по пространственному изображению или по ортогональным проекциям (эпюру Монжа) без дополнительных графических построений не представляется возможным.
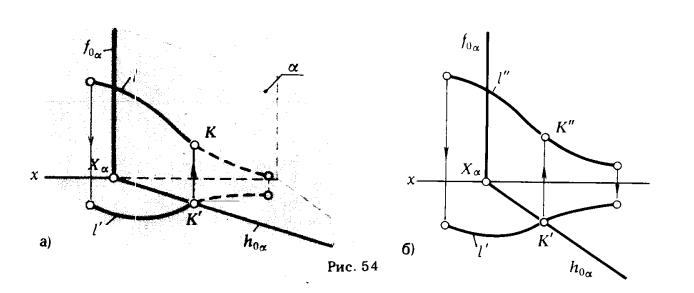
В то же время ситуация, заданная на рис. 54,а, позволяет сразу, без каких - либо дополнительных построений, получить ответ.
Для решения задачи используем инвариантное свойство 2г (см. § 6).
Точка К, в которой линия l пересекает плоскость α, как принадлежащая горизонтально проецирующей плоскости, будет иметь горизонтальную проекцию
К' на горизонтальном следе плоскости h0α: К' = l' ∩ h0α. Зная положение К', определяем К".
На рис. 54,б приведено решение этой задачи на эпюре Монжа.
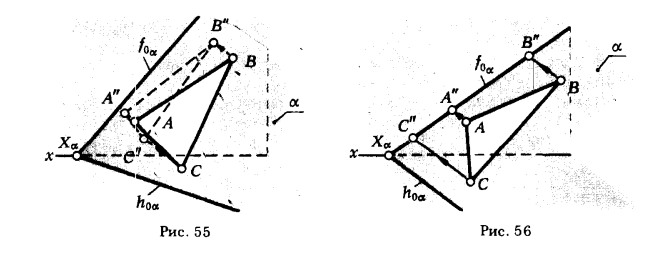
ПРИМЕР 2. Определить длины сторон ΔАВС и величины углов при его вершинах.
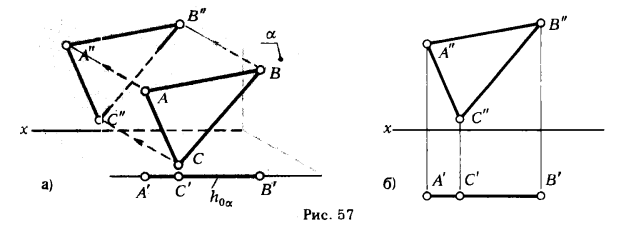
Очевидно, если плоскость ΔАВС (плоскость α) занимает произвольное положение относительно плоскостей проекций (рис. 55), или перпендикулярное к какой-либо плоскости (рис. 56), то для решения поставленной задачи необходимо выполнить определенные графические построения. В то же время ответ на поставленные вопросы может быть получен без каких-либо графических построений непосредственно из ортогональных проекций, если плоскость ΔАВС параллельна плоскости проекции (рис. 57,а,б). Это утверждение базируется на инвариантном свойстве 2д (см. § 6).
Приведенные примеры показывают, что проецируемая фигура может занимать по отношению к плоскости проекции или произвольное, или частное положение. В первом случае, как правило, получаются проекции, неудобные для решения задач. В то же время решение задачи значительно упрощается, когда мы имеем дело с частным расположением геометрических фигур относительно плоскости проекции (см. рис. 54 и 57). Наиболее выгодным частным положением проецируемой фигуры (в случае ортогонального проецирования), при котором получаются проекции фигуры, удобные для решения задач, следует считать:
а) положение, перпендикулярное к плоскости проекции, - при решении позиционных задач (см. рис. 54) *;
б) положение, параллельное плоскости проекции, - для решения метрических задач (см. рис. 57).
В связи с этим, естественно, возникает вопрос, каким путем можно получить удобные проекции для - решения поставленной задачи по заданным неудобным ортогональным проекциям?
Переход от общего положения геометрической фигуры к частному можно осуществить изменением взаимного положения проецируемой фигуры и плоскости проекции. При ортогональном проецировании это может быть достигнуто двумя путями:
во-первых, перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве;
во-вторых, выбором новой плоскости проекции, по отношению к которой проецируемая фигура, не меняющая своего положения в пространстве, окажется в частном положении.
Первый путь лежит в основе способа плоскопараллельного перемещения; второй - составляет теоретическую базу способа замены плоскостей проекций. Рассмотрим каждый из этих способов в отдельности.
1. Cпособ плоскопараллельного перемещения
Изменение взаимного положения проецируемой фигуры и плоскостей проекций способом плоскопараллельного перемещения осуществляется путем перемещения геометрической фигуры в новое положение так, чтобы траектории перемещения ее точек находились в параллельных плоскостях.
В зависимости от положения этих плоскостей по отношению к плоскостям проекций и вида кривой (траектории перемещения точки) различают несколько способов плоскопараллельного перемещения:
1. Способ параллельного перемещения.
Плоскости - носители траекторий перемещения точек параллельны плоскости проекции. Траектория - произвольная плоская линия.
2. Способ вращения вокруг оси, перпендикулярной к плоскости проекции.
Плоскости - носители траекторий перемещения точек параллельны плоскости проекции. Траектории - дуги окружностей, центры которых находятся на оси, перпендикулярной плоскости проекции.
3. Способ вращения вокруг оси, параллельной плоскости проекции (вращение вокруг линий уровня).
4. Способ вращения вокруг оси, принадлежащей плоскости проекции (вращение вокруг следа плоскости).
Рассмотрим каждый из этих способов в отдельности.
Способ параллельного перемещения
Для параллельного перемещения (переноса) справедливо утверждение, которое может быть выражено в виде следующей теоремы:ПодробнееСпособ вращения вокруг оси, перпендикулярной к плоскости проекции
Вращение вокруг оси, перпендикулярной к плоскости проекции, является частным случаем параллельного перемещения. Отличие от общего случая состоит лишь в том, что за траекторию перемещения точки берется не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между точкой и осью вращения.ПодробнееСпособ вращения вокруг оси, параллельной плоскости проекции (вращение вокруг линии уровня)
Эффективным приемом, упрощающим решение задач, связанных с определением метрических характеристик плоских фигур, является способ вращения этих фигур вокруг их линий уровня.ПодробнееСпособ вращения вокруг оси, принадлежащей плоскости проекции (совмещение)
Совмещение является частным случаем вращения плоскости вокруг горизонтали и фронтали.ПодробнееЗамена одной плоскости проекции
Пусть в системе плоскостей х·π2/π1 дана точка А и указаны ее проекции А' и А" (рис. 74,а). Проследим, как изменится положение проекций точки А, если плоскость π2 заменить новой плоскостью π3, перпендикулярной к π1 . Горизонтальная плоскость проекции не меняетПодробнееЗамена двух плоскостей проекций
Часто при определении действительной величины какой-либо геометрической фигуры или для получения более полного (наглядного) ее изображения замены одной плоскости проекций бывает недостаточно. В таких случаях приходится осуществлять замену двух плоскостей проекций.ПодробнееСочетание способа плоскопараллельного перемещения со способом замены плоскостей проекции
Пользуясь только одним способом плоскопараллельного перемещения или только одним способом замены плоскостей проекций, всегда мохсно перейти от произвольного расположения геометрическойПодробнееДругие способы преобразования ортогональных проекций
Кроме плоскопараллельного перемещения и замены плоскостей проекций начертательная геометрия располагает большим количеством различных способов получения новых, наиболее удобных для решения задач проекций по заданным неудобным.ПодробнееПриведение прямых линий и плоских фигур в частные положения относительно плоскостей проекций
Задание прямых линий и плоских фигур в частных положениях относительно плоскостей проекций (см. §§ 11, 19) значительно упрощает построения и решение задач, а подчас позволяет получить ответ или непосредственно по данному чертежу, или при помощи простейших построений.ПодробнееСпособ перемены плоскостей проекции
Общие сведения. Сущность способа перемены плоскостей проекций 2) заключается в том, что положение точек, линий, плоских фигур, поверхностей в пространстве остается неизменным, а система π1, π2 дополняется плоскостями, образующими с π1, или π2, или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.ПодробнееОсновы способа вращения
При вращении вокруг некоторой неподвижной прямой (ось вращения) каждая точка вращаемой фигуры перемещается в плоскости, перпендикулярной к оси вращения (плоскость вращения).ПодробнееВращение точки, отрезка прямой, плоскости вокруг оси, перпендикулярной к плоскости проекций
Вращение вокруг заданной оси. 1. Пусть точка А вращается вокруг оси, перпендикулярной к пл. π1 (рис. 212).ПодробнееПрименение способа вращения без указания на чертеже осей вращения, перпендикулярных к плоскости π1 или π2
Раньше (см. § 35) мы видели, что если вращать отрезок прямой линии или плоскую фигуру вокруг оси, перпендикулярной к плоскости проекций, то проекция на эту плоскость не изменяется ни по виду, ни по величине — меняется лишь положение этой проекции относительно оси проекций.ПодробнееВращение точки, отрезка прямой, плоскости вокруг оси, параллельной плоскости проекций, и вокруг следа плоскости
Поворот плоской фигуры вокруг ее горизонтали. Для определения формы и размеров плоской фигуры можно ее повернуть вокруг принадлежащей ей горизонтали так, чтобы в результате вращения фигура расположилась параллельно плоскости π1.ПодробнееПримеры решения задач с применением способов перемены плоскостей проекций и вращения
Построить проекции точки пересечения двух профильных прямых, лежащих в общей для них профильной плоскости.Подробнее