Способ параллельного перемещения
ТеорияДля параллельного перемещения (переноса) справедливо утверждение, которое может быть выражено в виде следующей теоремы:
при параллельном переносе геометрической фигуры относительно плоскости проекции проекция фигуры на эту плоскость хотя и ме-
няет свое положение, но остается конгруентной проекции фигуры в ее исходном положении
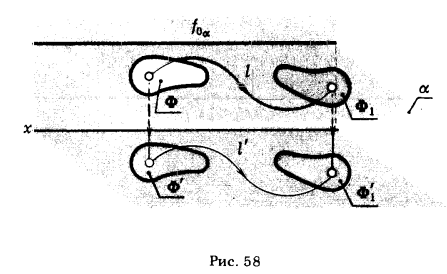
Докажем эту теорему для случая, когда проецируемая фигура плоская и ее плоскость принадлежит плоскости уровня Ф ⊆ α, плоскость α ||π1 (рис. 58). В этом случае на основании инвариантного свойства 2д (см. § 6) горизонтальная проекция Ф' будет конгруентна самой фигуре Ф (Ф' ≅ Ф).
При перемещении фигуры Ф в новое положение Ф1 фигура Ф1 будет конгруентна Ф, так как:
а) расстояние между точками фигуры не меняется;
б) в процессе перемещения фигура Ф все время остается в плоскости α.
В силу параллельности плоскостей α и π1 Ф'1 ≅ Ф1,но Ф1 ≅ Ф, а Ф ≅ Ф', следовательно, Ф'1 ≅ Ф'. Доказанная теорема будет справедлива и в случае, когда геометрическая фигура занимает произвольное положение относительно плоскости проекции.
Отметим еще два свойства параллельного перемещения:
1. При всяком перемещении точки в плоскости, параллельной плоскости проекции π1, ее фронтальная проекция перемещается по прямой, параллельной оси х.
2. В случае произвольного перемещения точки в плоскости, параллельной π2, ее горизонтальная проекция перемещается по прямой, параллельной оси X.
Справедливость отмеченных свойств может быть легко показана на простом примере.
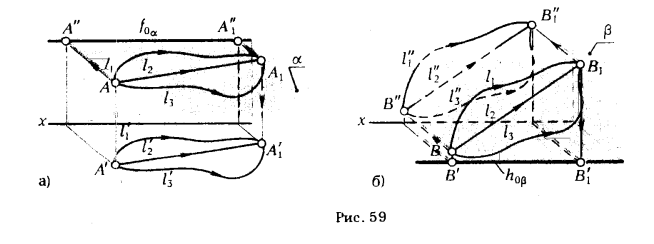
Возьмем плоскость α, параллельную горизонтальной плоскости проекции π1 (рис. 59). Пусть точка А ∈ α переместится из положения А в A1(А → A1 ). двигаясь в плоскости α по произвольной траектории (l1, l2 или l3). Очевидно, фронтальная проекция точки А" переместится в А"1, при этом [А" А"1] принадлежит следу f0α, который параллелен оси х ([А"А"1] ⊂ f0α || х).
На рис. 59,6 показано перемещение точки В ∈ β || π2. Из чертежа видно, что горизонтальная проекция траектории перемещения точки В из первоначального положения в новое В1 представляет |В'В'1| ⊂ h0β || х и не зависит от вида линии - траектории перемещения точки из положения В в B1 .
Пользуясь приведенной теоремой и отмеченными свойствами, легко построить новые проекции геометрической фигуры по заданным ее ортогональным проекциям, и, в частности, такие ее проекции, которые
соответствуют отмеченным выше (см. с. 48) частным положениям проецируемой фигуры по отношению к плоскости проекции.
Проследим на примерах использование способа параллельного перемещения для перевода произвольно расположенной геометрической фигуры в частное положение.
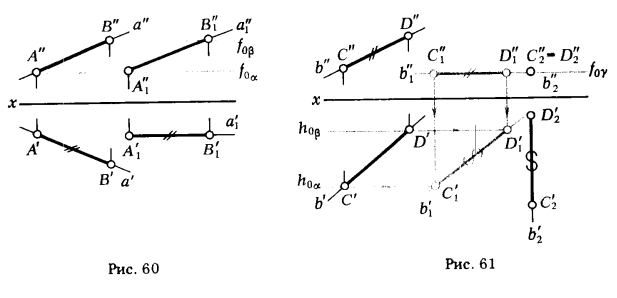
ПРИМЕР 1. [АB] прямой общего положения а перевести в положение, параллельное плоскости π2 (рис. 60).
У [АB], параллельного плоскости π2, горизонтальная проекция должна быть параллельна оси х. Поэтому переводим [A'В'] в новое положение [A'1В'1], параллельное оси х. Перемещение отрезка в новое положение осуществляем так, чтобы любые его точки двигались в плоскостях, параллельных плоскости π1 . При таком перемещении новая горизонтальная проекция конгруентна исходной [A'1В'1] ≅ [А'В'] (на основании теоремы с. 49).
Фронтальные проекции точек отрезка [А"В"] будут перемещаться в новое по
ложение по прямым, параллельным оси х (свойство 1,с.49).
На рис. 60 графические построения выполнены в указанной ниже последовательности :
1) через произвольную точку А'1 провели прямую а'1, параллельную оси х;
2) отложили на ней от точки А'1 отрезок [A'1B'1] ≅ [А 'В'];
3) из точек А'1 и В'1 восставили перпендикуляры к оси х и нашли точки пересечения их с соответствующими горизонтальными прямыми, проведенными через точки А" и В".
Полученные точки A'1, B'1 являются концами фронтальной проекции отрезка [А1В1], параллельного плоскости π2 .
Для перевода отрезка прямой, произвольно расположенной в пространстве, в положение, параллельное плоскости π2, потребовалось выполнить только одно перемещение отрезка параллельно плоскости проекции. Для перевода отрезка из общего положения в проецирую-
щее необходимо последовательно выполнить два его перемещения параллельно плоскостям проекции: вначале перевести отрезок в положение, параллельное плоскости π1 (или π2) путем перемещения параллельно плоскости π2 (или π1), затем перевести отрезок в положение, перпендикулярное π2 (или π1).
ПРИМЕР 2. [CD] прямой общего положения Ь перевести в положение ⊥ π2 (рис. 61).
На рис. 61 [CD] вначале переведен в положение ||π1([С1D1]), затем перемещением параллельно плоскости π1 - в положение ⊥ π2 ([C2D2 ] ) .
Зная характер геометрических построений, которые необходимо выполнить для перемещения отрезка из общего положения в проецирующее, можно легко перевести плоскость, произвольно расположенную в пространстве, в частное положение (параллельное или перпендикулярное плоскости проекции).
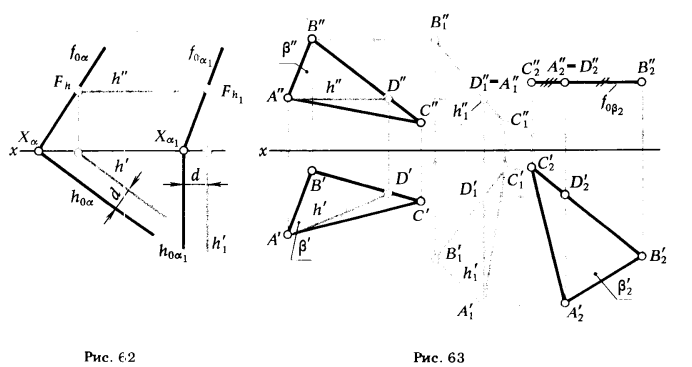
На рис. 62 показан перевод плоскости общего положения α(h0α, f0α) в новое α1 (h0α1, f0α1 ). при этом α1 ⊥ π2 .
Как видно из чертежа, перевод плоскости α в положение α1 осуществлен с помощью горизонтали h, которая переведена в положение h1 ⊥ π2, поэтому и α1 ⊥ π2. Следует обратить внимание на то, что расстояние d остается постоянным:
|h0αh'| = |h0α1h'1 |.
Рис. 63 дает представление о преобразовании ортогональных проекций ΔАВС, определяющего плоскость общего положения β, в проекции ΔА2В2С2, задающего плоскость β2 || π1 .
Геометрические построения выполнены в последовательности, указанной индексами, поставленными у проекций точек справа внизу. Выполненные на эпюре построения соответствуют перемещению плоскости в пространстве вначале || π1 во фронтально-проецирующее положение (ΔA1B1C1 ), затем перемещением || π2 плоскость треугольника переведена в положение || (ΔА2В2С2).