Способ вращения вокруг оси, параллельной плоскости проекции (вращение вокруг линии уровня)
ТеорияЭффективным приемом, упрощающим решение задач, связанных с определением метрических характеристик плоских фигур, является способ вращения этих фигур вокруг их линий уровня. Путем такого вращения можно плоскость, которой принадлежит рассматриваемая фигура, повернуть в положение, параллельное плоскости проекции. В этом случае ортогональная проекция любой принадлежащей плоскости фигуры будет конгруентна оригиналу и, следовательно, позволит определить все метрические характеристики проецируемой фигуры непосредственно по ее проекции без каких-либо дополнительных построений.
Очевидно, вращая плоскость вокруг горизонтали, можно перевести ее в положение, параллельное плоскости π1, и получить неискаженный вид горизонтальной проекции. Вращение плоскости вокруг фронтали позволяет перевести ее в положение, параллельное плоскости π2, что обеспечит получение неискаженного вида фронтальной проекции.
Каждая точка плоскости при ее вращении перемещается по окружности, принадлежащей плоскости, перпендикулярной к оси вращения. Центр окружности будет находиться на оси вращения, а величина радиуса вращения равна расстоянию от точки до оси вращения. Если за ось вращения взята горизонталь, то окружность, представляющая траекторию движения точки, будет проецироваться на плоскость π1 в отрезок прямой, перпендикулярной горизонтальной проекции горизонтали. На плоскость π2 окружность проецируется в эллипс, построение которого можно не делать. Точка пересечения горизонтальных проекций горизонтали и горизонтальной проекции окружности определяет горизонтальную проекцию центра вращения.
Аналогично, при вращении плоскости вокруг фронтали любая точка, принадлежащая плоскости, перемещается по окружности, которая проецируется на плоскость π2 в отрезок прямой, перпендикулярной фронтальной проекции фронтали. Фронтальная проекция центра вращения определяется пересечением фронтальных проекций фронтали и окружности.
Вращение точки вокруг горизонтали показано на рис. 69. Точка А при вращении вокруг горизонтали h будет перемещаться по окружности с, плоскость которой β перпендикулярна оси вращения h. Чтобы переместить точку в новое положение путем поворота ее вокруг h, необходимо найти положение центра вращения и определить величину радиуса вращения. Центр вращения О находится в точке пересечения оси вращения h с плоскостью β. Чтобы определить величину радиуса вращения ОА , необходимо построить в плоскости π1 прямоугольный ΔО'А'А*0. Для этого принимаем горизонтальную проекцию О'А' за катет прямоугольного треугольника; второй катет должен быть равен разности аппликат концов отрезка ОА: |z(·)А - z(·)O |= |А1|. Гипотенуза ΔО'А'А0 О'А0 = R. Новое, после поворота, положение точки А'1 находится в месте пересечения дуги окружности, проведенной из горизонтальной
* Величину отрезка [ОА] можно определить и другим путем, например, вращением его вокруг оси, перпендикулярной плоскости проекции; плоскопараллельным перемещением или, как это будет показано в § 13, с помощью замены плоскости проекции.
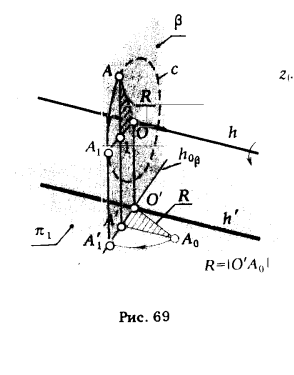
проекции центра вращения О' радиусом, равным |О'A0|, с горизонтальным следом h0β плоскости β.
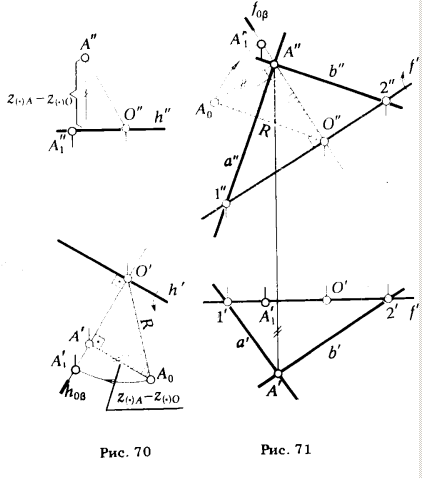
На рис. 70 описанные выше построения выполнены на эпюре Монжа. Характер и последовательность геометрических построений, которые необходимо выполнить для перемещения плоскости, произвольно расположенной в пространстве, в положение, параллельное плоскости проекции π2 , вращением вокруг линии уровня, показаны на рис. 71, на котором плоскость α, заданная пересекающимися прямыми а и b, переведена вращением вокруг своей фронтали f в положение, параллельное плоскости π2.
Плоскость α однозначно определяется также тремя точками 1,2 и А. Так как точки 1 и 2 принадлежат фронтали f, которая принята за ось вращения, то они не меняют своего положения в процессе преобразования. Поэтому, чтобы задать новое положение плоскости α1|| π2, достаточно осуществить поворот только одной точки А. Ниже приводится последовательность геометрических построений, которые необходимо выполнить для поворота точки А:
1) провести горизонтальную проекцию фронтали плоскости α - f'(1', 2' );
2) пользуясь точками 1', 2', найти точки 1", 2", определяющие фронтальную проекцию фронтали f";
3) найти проекции центра вращения (O', О"), для чего через А" провести прямую, перпендикулярную к f", и отметить точку пересечения перпендикуляра с f" - точку О";
4) определить величину радиуса вращения, как гипотенузу прямоугольного треугольника О"А"А0, у которого катет А"А0 = |У(·)А - У(·)O|;
5) из центра О" провести дугу радиусом О"А0, точка пересечения которой с прямой О"А" укажет положение А"1.
Точка А1 совместно с прямой f (точками 1, 2) определяет плоскость α1 || π2.