Касательные и нормали к пространственной кривой

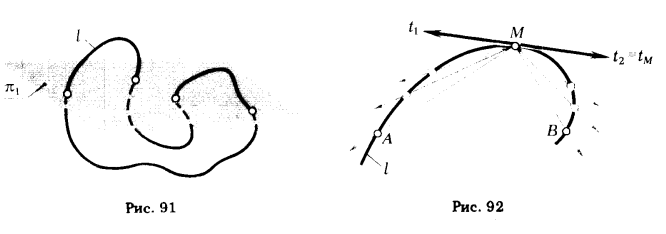
На рис. 92 показана пространственная кривая l. Возьмем на ней произвольную точку М и проведем через нее секущие [МА) и [МВ).

При приближении точки А к точке М [МА) будет поворачиваться вокруг точки М, и когда точка А совпадет с точкой М, [МА) достигнет своего предельного положения (луч t₁).

Предельное положение секущей в точке М называется полукасательной к кривой l в точке М.

* К алгебраическим линиям, в частности, относятся окружность, эллипс, парабола, гипербола, астроида, кардиоида и др.

** К трансцендентным линиям относятся синусоида, спираль архимеда, циклоида и др.

[МВ) при совпадении точки В с точкой М займет предельное положение t₂. Из чертежа видно, что в точке М к кривой l проведены две полукасательные, направленные в противоположные стороны. Полукасательные t₁ и t₂ образуют прямую, которую называют касательной к кривой в данной точке (t_M).

Через касательную к пространственной кривой в данной точке можно провести пучок плоскостей*. Одна из плоскостей этого пучка, называемая соприкасающейся плоскостью, играет особую роль при исследовании свойств пространственных кривых.

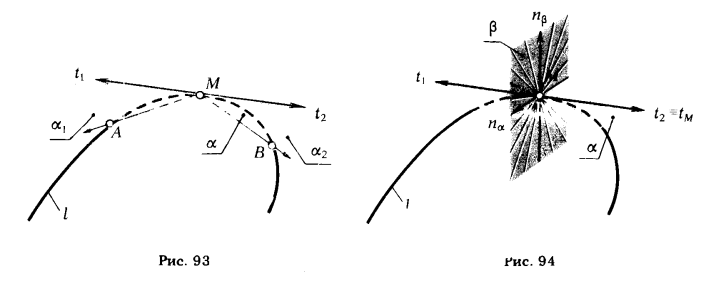
Подойти к понятию соприкасающейся плоскости можно путем следующих рассуждений: пусть дана пространственная кривая l (рис. 93). Возьмем на ней произвольную точку М и укажем полукасательные t₁ и t₂ к кривой l в этой точке. Через точку М проведем две секущие [МА) и [МВ). Обозначим полуплоскость, заданную полукасательной t₁ и секущей [МА), α₁ , а плоскость, определяемую полукасательной t₂ и [МВ), - α₂. При приближении точек А и В к точке М плоскости α₁ и α₂ будут проворачиваться вокруг полукасательных. Когда секущие займут положение полукасательных, плоскости α₁ и α₂ займут предельное положение.

Так как полукасательные принадлежат одной прямой, то плоскости α₁ и α₂ совпадут, образуя одну плоскость α, которую называют соприкасающейся плоскостью пространственной кривой в данной точке.

Соприкасающаяся плоскость может быть определена так же, как предельное положение плоскости, проходящей через три бесконечно близкие точки пространственной кривой линии.

Соприкасающаяся плоскость неразрывно связана с движущейся по кривой точкой. Так как каждая точка кривой имеет свою касательную (кроме особых точек), то соприкасающаяся плоскость при перемещении по кривой будет все время менять свое положение. При этом она будет не только следовать за касательной к кривой, но, одновременно, и вращаться вокруг нее.

К пространственной кривой линии l в любой ее точке (за исключением некоторых особых точек) можно провести пучок перпендикулярных к ней прямых (рис. 94) **. Множество этих перпендикуляров (нормалей) определяют плоскость, которую называют нормальной плоскостью β. Одна из нормалей этого множества, принадлежащая соприкасающейся плоскости, называется главной нормалью n_α.

* Пучком плоскостей называется множество всех плоскостей, проходящих через одну и ту же прямую а; прямая а называется осью этого пучка.

** Пучком прямых называется множество всех прямых плоскости, проходящих через данную точку М: точка М называется центром пучка.

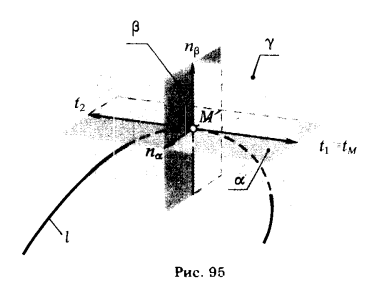
Другую нормаль этого множества, перпендикулярную к соприкасающейся плоскости, называют бинормалью η_β. Бинормаль ηβ и касательная t_M определяют плоскость γ, которую называют спрямляющей плоскостью кривой (рис. 95).

Трехгранник Френе. Три взаимно перпендикулярные плоскости α, β и γ (рис. 95), проходящие через одну точку пространственной кривой, образуют прямоугольный трехгранник, называемый основным или подвижным трехгранником. Его называют также трехгранником Френе *.

Трехгранник Френе используется в качестве системы плоскостей проекций, на которые проецируют пространственную кривую для изучения ее свойств. При этом плоскость α принимают за горизонтальную, плоскость γ за фронтальную и плоскость β за профильную плоскость проекции.

Дифференциальные свойства пространственной кривой исследуют по ее плоским проекциям на гранях трехгранника Френе.

П. ПЛОСКИЕ КРИВЫЕ ЛИНИИ

Кривая линия называется плоской, если все ее точки принадлежат одной плоскости.

Основные понятия и определения, приведенные на с. 69 для пространственных кривых, сохраняются с некоторыми изменениями и для плоских кривых линий; плоские кривые могут быть также алгебраическими и трансцендентными.

В первом случае уравнение кривой в декартовых координатах может быть представлено в форме f (х, у) = 0, где f(x, у) - целый многочлен от х и у.

Определения полу касательной и касательной в точке плоской кри-

* По имени французского математика Жана Фредерика Френе, предложившего его в 1847 г.

вой также совпадают с аналогичными определениями для пространственной кривой.

В отличие от пространственной кривой, для каждой точки которой может быть проведено множество перпендикулярных к ней прямых, образующих нормальную плоскость, плоская кривая в каждой ее точке имеет только одну нормаль - прямую, перпендикулярную к касательной в данной точке кривой и принадлежащую плоскости кривой.

В инженерной практике часто приходится проводить касательные и нормали к плоским кривым. Рассмотрим графические способы построения этих линий.