Прямоугольные аксонометрические проекции. Коэффициенты искажения и углы между осями

1. Возьмем плоскость аксонометрических проекций таким образом, чтобы она пересекала все три координатные оси (рис. 454, слева) в точках X, Y, Z. В случае прямоугольных аксонометрических проекций отрезок OO_α, перпендикулярен к плоскости α. Отрезки О_αХ, О_αY, O_αZ (аксонометрические проекции отрезков на осях) представляют собой катеты прямоугольных треугольников, а сами отрезки на осях координат — гипотенузы. Отсюда O_αX: ОХ = cosφ, O_αY: ОY= cosσ, 0_αZ :0Z =cosγ. Но эти отношения представляют собой коэффициенты искажения k, m и m. Следовательно, k = cosφ, m = cosσ, n = cosγ. Для отрезка OO_α косинусы углов φ₁,σ₁ и γ₁ (рис. 454, справа) дополнительных к углам φ,σ и γ являются направляющими

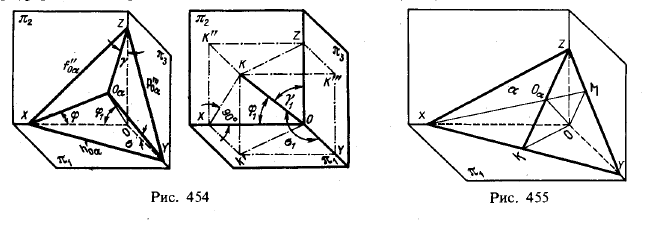
косинусами. Поэтому cos²φ₁ + cos²σ₁ + cos²γ₁ = 1 ²), а так как φ = π/2 — φ₁ и т. д., то sin²φ + sin²σ + sin²γ = 1, т. е. 1 — cos²φ + 1 — cos²σ + 1 — cos²γ = 1, откуда

¹) Древнегреческое «isos» — одинаковый; изометрическая проекция — проекция одинаковых коэффициентов искажения по всем трем осям; «di» — двойной; диметрическая проекция — проекция одинаковых коэффициентов искажения только по двум осям; «treis» — три; триметрическая проекция — проекция разных коэффициентов искажения по всем трем осям.

²) Напомним вывод этого соотношения (рис. 454, справа): ОК² = ОХ² + 0Y² + 0Z²; но ОХ = ОК·сosφ₁, 0У = OK·cosσ и OZ = OK·cosγ₁ откуда OK² = OK² cos²φ₁ + OK¹cos²σ₁ + OK²cos²γ₁ и (после сокращения на OK²) 1 = cos²φ₁ + cos²σ₁ + cos²γ₁>.

cos²φ + cos²σ + cos²γ = 2. Следовательно, k² + m² + n² = 2, т. е. для прямоугольной аксонометрической проекции сумма квадратов коэффициентов искажения равна двум.

2. Изометрическая проекция ¹). Так как k = m = m, то 3k² = 2, откуда

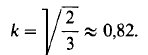
Это значит, что в прямоугольной изометрической проекции получается по каждой из осей (или по прямым, направленным параллельно этим осям) сокращение ≈0,82.

3. Диметрическая проекция. Два коэффициента искажения равны между собой,

а третий им не равен. Если взять k = n и выбрать m = 1/2k, то получим

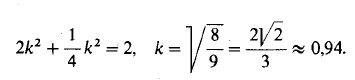
Следовательно, в прямоугольной диметрической проекции по двум осям (в данном случае по осям О_αх и O_αz) или по прямым, параллельным этим осям, получается сокращение ≈0,94, а по третьей оси (в данном случае по оси О_αу) — сокращение ≈0,47.

4. Плоскость аксонометрических проекций, пересекая плоскости координат, образует треугольник, называемый треугольником следов.

Докажем, что в прямоугольных аксонометрических проекциях аксонометрические оси являются высотами треугольника следов.

Действительно (рис. 455), если OO_α⊥α, то OK⊥XУ и по теореме о трех перпендикулярах ZK⊥XY. Аналогично, ХМ⊥YZ. Точка О_α является точкой пересечения высот (ортоцентром) треугольника следов.

Далее, в прямоугольных аксонометрических проекциях треугольник следов является остроугольным.

Действительно, в этом случае ортоцентр расположен внутри этого треугольника, а такое положение ортоцентра бывает только в остроугольном треугольнике.

Из этого вытекает, что углы XO_αZ, ХО_αY и YO_αZ — тупые. Действительно, так как треугольник следов остроугольный, то угол между высотами дополняет острый угол до 180°, например, ∠МО_αК = 180°— ∠ХО_αК; но ∠ХО_αК — острый, следовательно, ∠МО_αК — тупой.

Но из этого не следует, что в прямоугольной аксонометрической проекции можно применять лишь такую схему расположения осей, какая указана, например, на рис. 456, а. Пусть ось х продолжена за точку О_α вправо вверх и ось у продолжена за точку О_α влево вверх. В таком случае угол между продленными осяМи х и у останется тупым, но углы, образованные ими с осью z, окажутся острыми. Однако нетрудно установить, что в прямоугольной аксонометрической проекции выбор осей все же ограничен, а именно необходимо, чтобы тупой угол между двумя осями

¹) Термин «изометрические проекции» был впервые предложен в 1820 г. в докладах Фейрича (William Farich), прочитанных в Кембридже (Англия). В этих докладах Фейрич изложил теорию изометрических проекций; он же применил эти проекции в технике и широко их популяризировал. На русском языке сведения о прямоугольной изометрической проекции были впервые изложены в статье профессора Петербургского института инженеров путей сообщения А. X. Редера (1809 — 1872) в 1855 г. Более углубленное изложение вопроса об изометрической проекции как частном случае прямоугольных аксонометрических проекций дал Н. И. М а к а р о в, а затем В. И. Курдюмов, вообще посвятивший аксонометрическим проекциям ряд работ. В. И. Курдюмов предложил применять специальную бумагу с нанесенной на ней сеткой прямых линий, соответствующих направлениям осей в изометрической проекции. Мысль о такой бумаге для выполнения на ней эскизов в изометрической проекции была подсказана В. И. Курдюмову его практической инженерной работой.

разделялся продолжением третьей оси, а острый угол между двумя осями не мог быть разделен продолжением третьей оси.

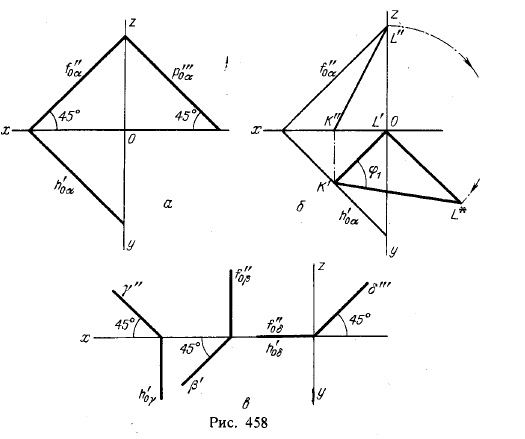
5. Положим, что заданы оси для прямоугольной аксонометрической проекции (рис. 456, а). Требуется определить коэффициенты искажения для данного расположения осей.

Прежде всего построим некоторый треугольник, в котором высоты направлены соответственно параллельно данным осям (рис. 456,6). Этот треугольник

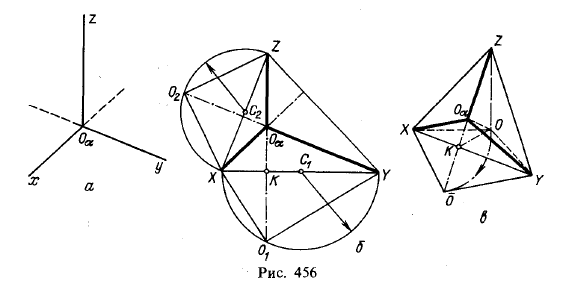
играет роль треугольника следов. Угол ХО_αY получен как проекция прямого угла между осями х и у в пространстве. Совместим в плоскости чертежа оба угла: ∠XO_αY и ∠XOY, повернув ∠XOY вокруг прямой ХУ до совмещения с пл. α (рис. 456, в). На рис. 456,6 показано, что, разделив XY точкой С₁ пополам и проведя полуокружность из этой точки радиусом С₁Х, мы можем спроецировать точку О_α по перпендикуляру к XY на полуокружность. Точка O₁ является вершиной прямого угла между осями х и у в пространстве после поворота.

Теперь искомые коэффициенты искажения определяются из соотношений О_αХ : O₁X = k и O_αY: O₁Y = m. Для определения коэффициента п можно применить формулу k² + m² + n² = 2 или построить полуокружность на XZ, как на диаметре, и взять отношение О_αХ : О₂Х = n.

6. Выше (с. 239) были выведены значения коэффициентов искажения для прямоугольных изометрической и диметрической проекций. По этим значениям коэффициентов искажения можно определить величины углов между осями для этих прямоугольных аксонометрических проекций из треугольников следов ¹).

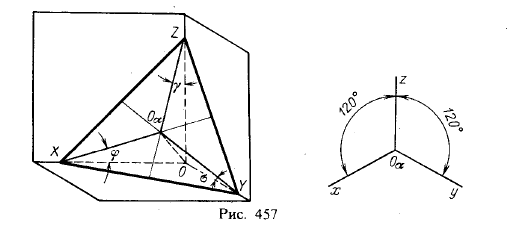
Изометрическая проекция (рис. 457). Мы рассматриваем прямоугольную проекцию; следовательно, прямая ОО_α перпендикулярна к плоскости, в которой расположен треугольник следов.

Коэффициенты искажения в изометрической проекции равны между собой: k = m = n; следовательно, cosφ = cosσ = cosγ и φ = σ = γ (углы острые).

Из этого следует, что треугольник следов для изометрической проекции равносторонний. А из этого вытекает, что в треугольнике следов каждый из углов XO_αZ, XO_αY, YO_αZ равен 120°.

Итак, для изометрической проекции получается расположение осей, указанное на рис. 457 справа.

¹) Точнее, из треугольников, подобных треугольникам следов. Построение осей в прямоугольной аксонометрической проекции по заданным коэффициентам искажения вообще можно производить на основании теоремы Вейсбаха: «В прямоугольной аксонометрической проекции аксонометрические оси являются биссектрисами углов треугольника, стороны которого пропорциональны квадратам коэффициентов искажения». Интересующихся доказательством отсылаем к книге, указанной в сноске на с. 237.

Плоскость изометрических проекций, пересекающая положительные полуоси х, у, z изобразится в системе ортогональных проекций, как это показано на рис. 458, а. Эта плоскость образует с каждой из координатных плоскостей угол &φ₁ ≈55°, точнее, 54°45'.

Очевидно, плоскости, расположенные подобно указанным на рис. 458, в, и лежащие в них фигуры изобразятся в изометрической проекции в виде прямой линии.

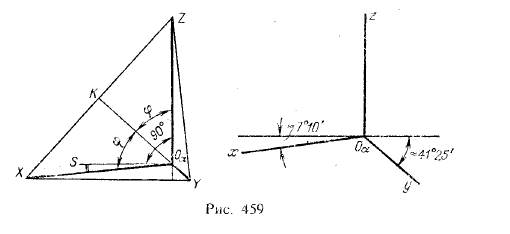
Диметрическая проекция. Здесь два из трех коэффициентов искажения равны между собой; мы будем рассматривать случай, когда k = n, k = 2m. В этом случаеугол между аксонометрическими осями O_αz и О_αу должен быть равен 131 °25', а ось0_αх составляет с перпендикуляром к оси 0_αz угол 7° 10'.

Докажем это. Пусть k = n и, следовательно, φ = γ и ОХ = OZ (рис. 457, слева). Принимая отрезок ОХ за единицу, получим XZ = √2. Рассматривая диметрическую проекцию, в которои k = n2√23 и m = √23, мы можем написать

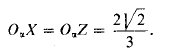
Так как ОХ = OZ, то XY = ZY, т.е. треугольник XYZ в данном случае равнобедренный.

В этом треугольнике (рис. 459) высота YK делит пополам сторону XZ, т.е.

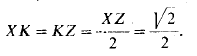
Из рассмотрения прямоугольного треугольника O_αKZ следует

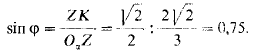
Угол φ≈48°35'; 2φ = 97°10'. Из рисунка видно, что ∠S0_αX≈7°10', так как O_αS⊥0_αZ.

Далее замечаем, что

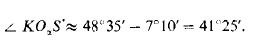
Итак, мы получили указанное на рис. 459 справа расположение осей для диметрической проекции, у которой коэффициенты искажения составляют отношение 1 :0,5 : 1.

Можно построить ось O_αх, приняв tg7°10' равным 1/8, и ось О_αу, приняв tg41 °25' равным 7/8. Ось О_αу может быть проведена и другим способом — как продолжение биссектрисы угла zO_αx (см. рис. 459, слева). Это предпочтительно.

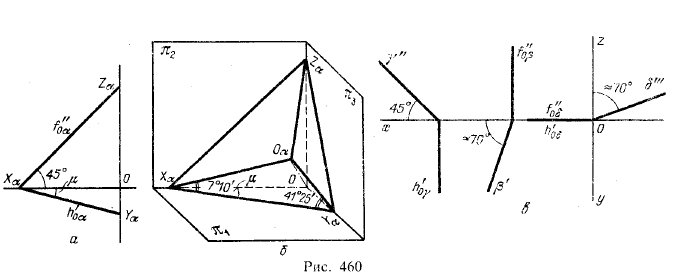
Если плоскость рассматриваемой нами диметрической проекции, пересекающую положительные полуоси х, у, z, изобразить в системе ортогональных проекций, то получится чертеж, показанный на рис, 460,a, причем угол μ≈20°40' (О У_α:ОХ_α = tgμ ≈ 0,377).

Итак, если плоскость диметрической проекции изображаете» в системе ортогональных проекций, то надо (см. рис. 460,а) отложить OZ_α = ОX_α и ОY_α ≈0,377·OX_α, или, округленно, 0,4·ОХ_α.

Очевидно, плоскости, расположенные подобно указанным на рис. 460,а, и лежащие в них фигуры изобразятся в диметрической проекции в виде прямой линии.

Отрезки, расположенные параллельно координатным осям в пространстве, претерпевают при аксонометрическом проецировании сокращение, выражаемое соответствующими коэффициентами искажения. Но в числе отрезков, расположенных в пространстве, имеются такие, размер которых не изменяется в аксонометрической их проекции. Это отрезки, расположенные в пространстве параллельно какой-либо из сторон треугольника следов. Действительно, каждый отрезок, расположенный, например, параллельно следу XY (рис. 457, слева), и в том числе сам отрезок XY сохраняет свою величину и в аксонометрической проекции. Но в прямоугольной аксонометрической проекции эти отрезки получаются расположенными перпендикулярно к аксонометрическим осям, как прямые, параллельные сторонам треугольника следов.

Мы ограничимся рассмотрением указанных двух аксонометрических прямоугольных проекций — изометрической и диметрической с соотношением коэффициентов искажения 1:0,5:1 и с осями, расположенными так, как это указано на рис. 459. В дальнейшем, применяя название изометрическая и диметрическая проекции, мы будем иметь в виду именно пи разобранные нами прямоугольные аксонометрические проекции.

В практике построения указанных проекций допускают следующие отступления :

1) в изометрической проекции по большей части не применяют коэффициентов искажения 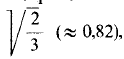, заменяя их приведенными коэффициентами, равными единице;

2) в диметрической проекции обычно не применяют коэффициентов искажения 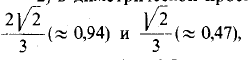, а берут вместо них приведенные коэффициенты соответственно 1 и 0,5.

Замена значений натуральных коэффициентов искажения более удобными числами (приведенными коэффициентами искажения) представляет значительные удобства при практических построениях. Получающееся при этом некоторое увеличение изображений, менее заметное в диметрической проекции, чем в изометрической, может оказаться неприемлемым лишь в особых случаях построений; тогда должны быть применены натуральные коэффициенты искажения.

Удлинение отрезков в изометрической проекции, построенной по приведенным коэффициентам искажения, выражается отношением 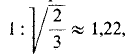а в диметрической проекции — отношением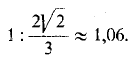

Например, отрезки, параллельные в пространстве сторонам треугольника следов и, следовательно, откладываемые в аксонометрической проекции по направлениям, перпендикулярным к аксонометрическим осям, удлиняются в изометрической проекции в 1,22 раза по сравнению с натуральной величиной, а в диметрической проекции — в 1,06 раза.