Точка в системе двух плоскостей проекций π1, π2
ТеорияВыше (§ 2) было сказано, что проекция точки не определяет положения точки в пространстве, и чтобы, имея проекцию точки, установить это положение, требуются дополнительные условия. Например, дана прямоугольная проекция точки на горизонтальной плоскости проекций и указано удаление этой точки от плоскости числовой отметкой; плоскость проекций принимается за «плоскость нулевого уровня», и числовая отметка считается положительной, если точка в пространстве выше плоскости нулевого уровня, и отрицательной, если точка ниже этой плоскости.
На этом основан метод проекции с числовыми отметками 1)
В дальнейшем изложении определение положения точек в пространстве будет производиться по их прямоугольным проекциям на двух и более плоскостях проекций.
На рис.9 изображены две взаимно перпендикулярные плоскости. Примем их за плоскости проекций. Одна из них, обозначенная буквой π1, расположена горизонтально; другая, обозначенная буквой π2,— вертикально. Эту плоскость называют фронтальной плоскостью проекций, пл. π1, называют горизонтальной плоскостью проекций. Плоскости проекций π1 и π2 образуют систему π1, π2.
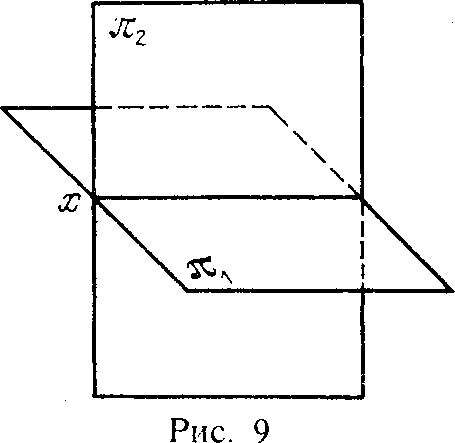
Линия пересечения плоскостей проекций называется осью проекций. Ось проекций разделяет каждую из плоскостей π1 и π2 на полуплоскости. Для этой оси будем применять обозначение x или обозначение в виде дроби π2/π1. Из четырех двугранных углов, образованных плоскостями проекций, считается первым тот, грани которого на рис.9 имеют обозначения π1 и π2.
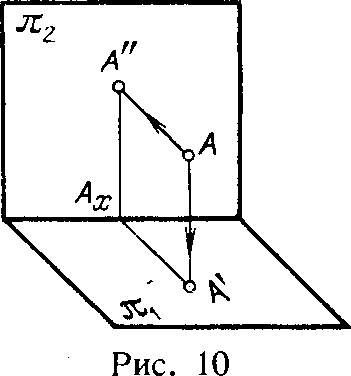
На рис.10 показано построение проекций некоторой точки А в системе π1, π2. Проведя из А перпендикуляры к π1 и π2, получаем проекции точки А: горизонтальную, обозначенную А', и фронтальную, обозначенную А".
Проецирующие прямые, соответственно перпендикулярные к π1 и π2, определяют плоскость, перпендикулярную к плоскостям и к оси проекций. Эта плоскость в пересечении с π1 и π2 образует две взаимно перпендикулярные прямые А'Аx и А"Аx, пересекающиеся в точке Аx на оси проекций. Следовательно, проекции некоторой точки получаются расположенными на прямых, перпендикулярных к оси проекций и пересекающих эту ось в одной и той же точке.
1) Метод проекций с числовыми отметками в программу излагаемого курса не входит. Интересующихся отсылаем к книгам по начертательной геометрии для строительных и архитектурных специальностей.
Если даны проекции А' и А" некоторой точки А (рис.11), то, проведя перпендикуляры — через А' к пл.π1 и через А" к пл. π2 — получим в пересечении этих перпендикуляров определенную точку. Итак, две проекции точки вполне определяют ее положение в пространстве относительно данной системы плоскостей проекций.
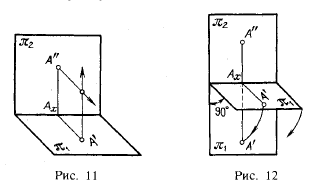
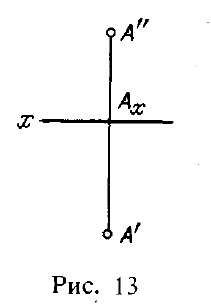
Повернув пл.π1 вокруг оси проекций на угол 90° (как это показано на рис.12), получим одну плоскость — плоскость чертежа; проекции А" и А' расположатся на одном перпендикуляре к оси проекций (рис. 13) — на линии связи. В результате указанного совмещения плоскостей π1 и π2 получается чертеж, известный под названием эпюр 1) (эпюр Монжа). Это чертеж в системе 1, π2 (или в системе двух прямоугольных проекций).
Перейдя к эпюру, мы утратили пространственную картину расположения плоскостей проекций и точки. Но, как увидим дальше, эпюр обеспечивает точность и удобоизмеримость изображений при значительной простоте построений. Чтобы представить по нему пространственную картину, требуется работа воображения: например, по рис.13 надо представить картину, изображенную на рис.10.
Так как при наличии оси проекций положение точки А относительно плоскостей проекций π1 и π2 установлено, что отрезок А'Аx выражает расстояние точки А от плоскости проекций π2, а отрезок А"Аx — расстояние точки А от плоскости проекций π1. Так же можно определить расстояние точки А от оси проекций. Оно выражается гипотенузой треугольника, построенного по катетам А'Аx и А"Аx (рис.14): откладывая на эпюре отрезок А"А, равный А!Аx, перпендикулярно к А"Аx, получаем гипотенузу ААx, выражающую искомое расстояние.
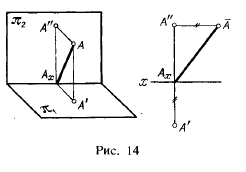
Следует обратить внимание на необходимость проведения линии связи между проекциями точки: только при наличии этой линии, взаимосвязывающей проекции, получается возможность установить положение определяемой ими точки.
Условимся в дальнейшем эпюр Монжа, а также проекционные чертежи, в основе которых лежит метод Монжа (см. § 3), называть одним словом — чертеж и понимать это только в указанном смысле. В других случаях применения слова «чертеж» оно будет сопровождаться соответствующим определением (перспективный чертеж, аксонометрический чертеж и т. п.).
1)Épure(франц.) — чертеж, проект. Иногда вместо «эпю́р» пишут и произносят «эпюра», что соответствует не произношению слова épure, а женскому роду этого слова во французском языке.