Точка на прямой. Следы прямой
ТеорияНа рис. 60 дан чертеж некоторой прямой общего положения, проходящей через точку А. Если известно, что точка В принадлежит этой прямой и что горизонтальная проекция точки В находится в точке В', то фронтальная проекция В" определяется так, как показано на рис. 60.
На рис. 61 показано построение точки на профильной прямой. Положим, что задана проекция С" этой точки; надо найти ее горизонтальную проекцию. Построение выполнено при помощи профильной проекции А'”В'” отрезка АВ, взятого на профильной прямой. Ход построения показан стрелками. Сначала определена проекция С'", а по ней — искомая проекция С'.
Одним из свойств параллельного проецирования является то, что отношение отрезков прямой линии равно отношению их проекций (рис. 62): AC/CB= A°C°/C°B°, так
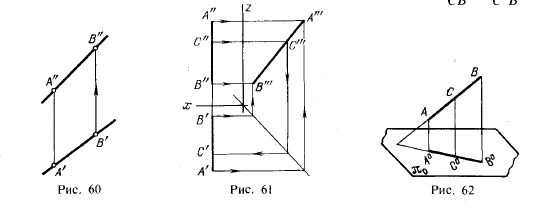
как прямые АА°, СС° и ВВ° параллельны между собой. Аналогично, отношение отрезков на проекции прямой линии равно отношению отрезков на этой прямой. Если бы точка делила пополам отрезок прямой, то проекция этой точки также делила бы проекцию отрезка пополам, и наоборот.
Из сказанного следует, что на рис. 61 деление проекций А"В" и А'В' точками С" и С' соответствует делению в пространстве отрезка АВ точкой С в том же отношении. Этим можно воспользоваться для более простого построения точки на профильной прямой. Если (как и на рис. 61) на проекции А"В" (рис. 63) задана проекция С", то, очевидно, надо разделить А'В' в том же отношении, в каком точка С" делит проекцию А"В". Проведя из точки А' некоторую вспомогательную прямую, откладываем на ней А'1 = А"С" и 1—2 = С"В". Проводим прямую В'2 и параллельно ей через точку 1 прямую до пересечения с А'В' в точке С'. Эта точка представляет собой искомую горизонтальную проекцию точки С, принадлежащей отрезку АВ.
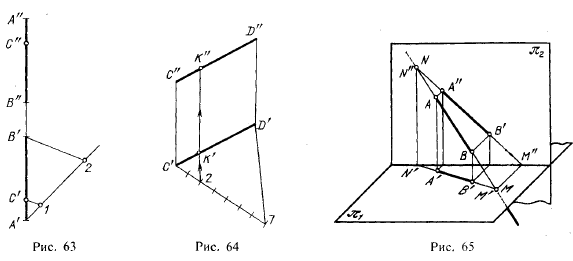
На рис. 64 дан пример деления отрезка прямой линии в некотором заданном отношении.
Отрезок CD разделен в отношении 2:5. Из точки С' проведена вспомогательная прямая, на которой отложено семь (2 + 5) отрезков произвольной длины, но равных между собой. Проведя отрезок D'7 и параллельно ему через точку 2 прямую, получаем точку К', причем С'К': K'D' = 2: 5; затем находим К". Точка К делит отрезок CD в отношении 2:5.
На рис. 65 показаны точки М и N, в которых прямая, заданная отрезком АВ, пересекает плоскости проекций. Эти точки называются следами: точка М — горизонтальный след прямой, точка N — ее фронтальный след.
Горизонтальная проекция горизонтального следа (точка М') совпадает с самим следом, а фронтальная проекция этого следа М" лежит на оси проекций. Фронтальная проекция фронтального следа N" совпадает с точкой N, а горизонтальная проекция N' лежит на той же оси проекций.
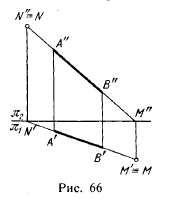
Следовательно, чтобы найти горизонтальный след, надо (рис. 66) продолжить фронтальную проекцию А"В" до пересечения с осью π2/π1 и через точку М" (фронтальную проекцию горизонтального следа) провести перпендикуляр к оси π2/π1 до пересечения с продолжением горизонтальной проекции А'В'. Точка М' — горизонтальная проекция горизонтального следа; она совпадает с самим следом (≡ знак совпадения).
Для нахождения фронтального следа продолжаем горизонтальную проекцию А'В' до пересечения с π2/π1 через точку N' (горизонтальную проекцию фронтального следа) проводим перпендикуляр до пересечения с продолжением фронтальной проекции А"В". Точка N" — фронтальная проекция фронтального следа; она совпадает с самим следом.
По положению точек М и N можно судить, к каким четвертям пространства отнесена данная прямая. На рис. 65 прямая АВ проходит через IV, I и II четверти.
Прямая не имеет следа на плоскости проекций в том случае, когда она параллельна этой плоскости.
На рис. 67 прямая пересекает не только пл.π1 и π2, но и пл. π3. Точка Р — профильный след прямой, т. е. след на профильной плоскости проекций. Этот след совпадает с его собственной проекцией на пл. π3, а фронтальная и горизонтальная проекции его лежат соотвегственно на осях z и у.
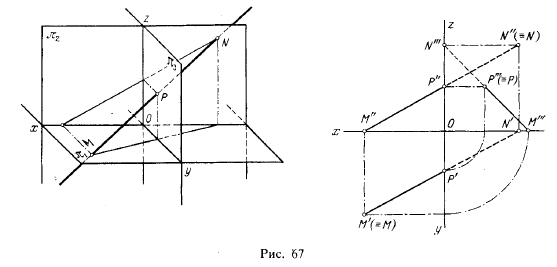
В данном случае прямая проходит за точкой Р через пятый октант и, встречая далее пл. π2, уходит в шестой октант; прямая из первого октанта выходит в четвертый октант 1).
Соответствующий чертеж дан на рис. 67 справа. Прямая показана в первом октанте — проекции М'Р'. М"Р" п М"'Р"' и в пятом октанте — проекции P'N', P"N" и P"'N"'.
Если плоскости проекций принять за плоскости координат, то у горизонтального следа прямой координата z = 0, у фронтального следа у = 0, у профильного следа х = 0.
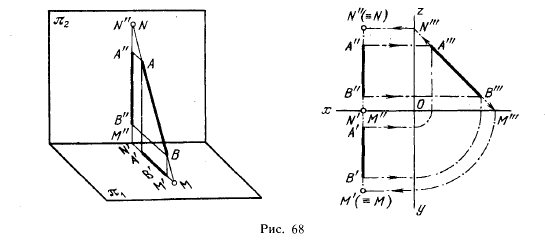
Построение следов профильной прямой (рис. 68) может быть выполнено следующим способом (рис. 68, справа).
1) Условимся показывать на чертежах сплошными линиями те проекции, которые соответствуют положению ^отрезка в первой четверти или в первом октанте.
Строим профильную проекцию (А"'В"'), определяем положение профильных проекций горизонтального следа (М'") и фронтального следа (N'") и затем находим положение остальных проекций этих следов (последовательность построения на чертеже показана стрелками).
ВОПРОСЫ К §§ 10-12
- При каком положении относительно плоскостей проекций прямая называется прямой общего положения?
- Как доказывается, что чертеж, содержащий две связанные между собой проекции в виде отрезков прямой линии, выражает именно отрезок прямой линии?
- Как выражается соотношение между проекцией отрезка прямой и самим отрезком?
- Как расположена прямая в системе π1,π2, π3, если все три проекции отрезка этой прямой равны между собой?
- Как построить профильную проекцию отрезка прямой общего положения по данным фронтальной и горизонтальной проекциям?
- Как выполнить построение по вопросу 5 на чертеже без осей проекций?
- Какие положения прямой линии в системе π1,π2, π3 считаются «особыми» (иначе — «частными»)?
- Как располагается фронтальная проекция отрезка прямой линии, если его горизонтальная проекция равна самому отрезку?
- Как располагается горизонтальная проекция отрезка прямой линии, если его фронтальная проекция равна самому отрезку?
- Какое свойство параллельного проецирования касается отношения отрезков прямой линии?
- Как разделить на чертеже отрезок прямой линии в заданном отношении?
- Что называется следом прямой линии на плоскости проекций?
- Какая координата равна нулю: а) для фронтального следа прямой, б) для горизонтального следа прямой?
- Где располагается горизонтальная проекция фронтального следа прямой линии?
- Где располагается фронтальная проекция горизонтального следа прямой линии?
- Может ли быть случай, когда прямая линия в системе π1,π2, π3 имеет следы на каждой к: этих плоскостей, сливающиеся в одну точку?