Взаимное положение двух прямых

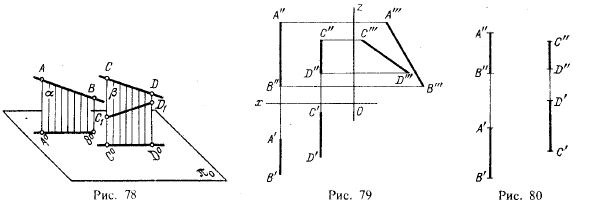
Параллельные прямые. К числу свойств параллельного проецирования относится следующее: проекции двух параллельных прямых параллельны между собой. Если (рис. 78) прямая АВ параллельна прямой CD, то проецирующие плоскости ? и ? параллельны между собой и при пересечении этих плоскостей с плоскостью проекций π₀ получаются параллельные между собой проекции А⁰В⁰ и C⁰D⁰.

Однако, хотя А⁰В⁰|| C⁰D⁰ (рис. 78), прямые, для которых А⁰В⁰и C⁰D⁰ являются проекциями, могут быть не параллельны между собой: например, прямая АВ не параллельна прямой C₁D₁.

Из указаннш о свойства параллельного проецирования следует, что горизонтальные проекции параллельных прямых параллельны между собой, фронтальные проекции параллельны между собой и профильные проекции параллельны между собой.

Справедливо ли обратное заключение, т. е. будут ли параллельны две прямые в пространстве, если на чертеже их одноименные проекции попарно параллельны?

Да,, если даны параллельные между собой проекции на каждой из трех плоскостей проекций π₁, π₂ и π₃. Но если даны параллельные между собой проекции прямых лишь на двух плоскостях проекций, то этим параллельность прямых в пространстве подтверждается всегда для прямых общего положения и может не подтвердиться для прямых, параллельных одной из плоскостей проекций.

Пример дан на рис. 79. Хотя профильные прямые АВ и CD заданы проекциями А'В', А"В" и CD', C"D", между собой параллельными, но самые прямые не параллельны — это видно из взаимного расположения их профильных проекций, построенных по заданным проекциям.

Итак, вопрос был решен при помощи проекций прямцх на той плоскости проекций, по отношению к которой данные прямые параллельны.

На рис. 80 показан случай, когда можно установить, что профильные прямые АВ и CD не параллельны между собой, не прибегая к построению третьей проекции: достаточно обратить внимание на чередование буквенных обозначений.

Если через данную точку А требуется провести прямую, параллельную данной прямой LM, то (рис. 81, слева) построение сводится к проведению через точку А" прямой, параллельной L"M", и через точку А' прямой, параллельной L'M'.

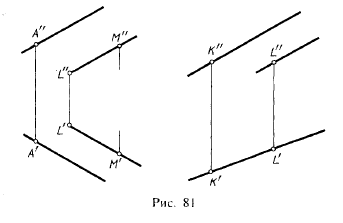
В случае, изображенном на рис. 81 справа, параллельные прямые расположены в общей для них проецирующей плоскости, перпендикулярной к пл. π₁. Поэтому горизонтальные проекции этих прямых расположены на одной прямой.

Пересекающиеся прямые. Если прямые линии пересекаются, то их одноименные проекции пересекаются между собой в точке, которая является проекцией точки пересечения этих прямых.

Действительно (рис. 82), если точка К принадлежит обеим прямым АВ и CD, то проекция этой точки должна быть точкой пересечения проекций данных прямых.

Заключение о том, что данные на чертеже прямые пересекаются между собой, можно сделать всегда по отношению к прямым общего положения, независимо от того, даны ли проекции на трех или двух плоскостях проекций. Необходимым и достаточным условием является лишь то, чтобы точки пересечения одноименных

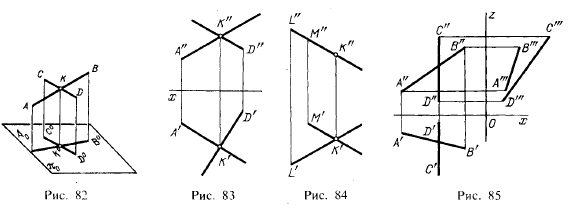
проекций находились на одном и том же перпендикуляре к соответствующей оси проекций (рис. 83) или, на чертеже без оси проекций (рис. 84), эти точки оказались бы на линии связи установленного для нее направления. Но если одна из данных прямых параллельна какой-либо из плоскостей проекций, а на чертеже не даны проекции на этой плоскости, то нельзя утверждать, что такие прямые пересекаются между собой, хотя бы и было соблюдено указанное выше условие. Например, в случае, данном на рис. 85, прямые АВ и CD, из которых прямая CD параллельна пл.π₃, не пересекаются между собой; это может быть подтверждено построением профильных проекций или применением правила о делении отрезков в данном отношении.

Изображенные на рис. 84 пересекающиеся прямые расположены в общей дня них проецирующей плоскости, перпендикулярной к пл. π₂. Поэтому фронтальные проекции этих прямых расположены на одной прямой.

Скрещивающиеся прямые. Скрещивающиеся прямые линии не пересекаются и не параллельны между собой. На рис. 86 изображены две скрещивающиеся прямые общего положения: хотя одноименные проекции и пересекаются между собой, но точки их пересечения не могут быть соединены линией связи, параллельной линиям связи L"L' и М"М', т. е. эти прямые не пересекаются между собой. Прямые, изображенные на рис. 79, 80 и 85, также скрещивающиеся.

Как надо рассматривать точку пересечения одноименных проекций скрещивающихся прямых? Она представляет собой проекции двух точек, из которых одна

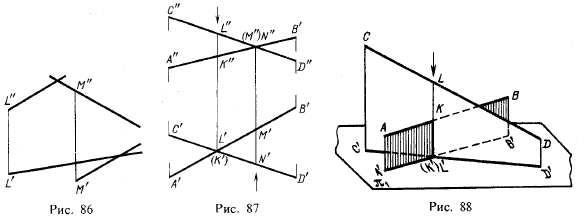
принадлежит первой, а другая — второй из этих скрещивающихся прямых. Например, на рис. 87 точка с проекциями К” и К' принадлежит прямой АВ, а точка с проекциями L" и L' принадлежит прямой CD. Эти точки одинаково удалены от пл. π₂, но расстояния их от пл. π₁ различны: точка с проекциями L" и L' дальше от π₁, чем точка с проекциями К" и К' (рис. 88).

Точки с проекциями М", М' и N”, N' одинаково удалены от пл. π₁ но расстояния этих точек от пл. π₂ различны.

Точка с проекциями L" и L', принадлежащая прямой CD, закрывает собой точку с проекциями К" и К' прямой АВ по отношению к пл. π₁; соответствующее направление взгляда показано стрелкой у проекции L". По отношению к пл. π₂ точка с проекциями N" и N' прямой CD закрывает собой точку с проекциями М" и М' прямой АВ; направление взгляда указано стрелкой внизу, у проекции N'.

Обозначения проекций «закрытых» точек помещены в скобках ¹).