Чертежи без указания осей проекций
ТеорияВ дальнейшем изложении наряду с чертежами, содержащими оси проекций, будут применяться чертежи без указания осей.
Из сравнения чертежей на рис. 42 следует, что в одном случае положение плоскостей π1 и π2 установлено проведением линии их пересечения и что установлены расстояния точки А от этих плоскостей. На втором же чертеже на рис. 42 вопрос о расстояниях точки А от плоскостей π1 и π2 отпадает, так как ось проекций отсутствует; рассматривается некоторая точка А, заданная своими проекциями, безотносительно к тому, где находятся плоскости проекций. При этом, конечно, тем большее значение приобретает линия связи проекций, ее направление и правильное проведение.
Можно ли, имея чертеж без указания оси проекций, ввести эту ось и тем задать расстояния точки от условно выбранных плоскостей π1 и π2? Да, можно. Вводя ось, надо ее провести обязательно перпендикулярно к линии связи, но безразлично,
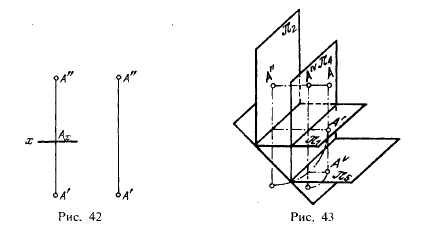
в какой именно точке на этой линии (если не указывается какое-либо условие). При этом положение проекций не изменится. Действительно, проведя ось проекций, мы выбираем некоторое положение двугранного угла π1,π2 относительно данной точки А (рис. 43). Перенесение оси на чертеже вверх или вниз соответствует параллельному перемещению в пространстве двугранного угла π1π2 в новое положение (на рис. 43 положение π4π5) в направлении биссекторной плоскости двугранного угла 1), смежного с углом π1π2.
Введение оси проекций (а это делается обычно в соответствии с каким-либо условием) было показано на рис. 37 и 38: оси π3/π1 и π2/π5. Здесь оси были нужны для построения: от них отсчитывались размеры. Вообще, оси, если их рассматривать в первоначальном значении линий пересечения плоскостей проекций, помогают представлению пространственной картины по чертежу.
Базы отсчета размеров являются неотъемлемой составляющей технических чертежей; выбор положения баз не является ограниченным и определяется, исходя из необходимости и целесообразности.
1) Биссекторная плоскость двугранного угла — плоскость, проходящая через ребро двугранного угла и делящая его пополам. Bissektor (лат.) — надвое рассекающий.
На рис. 44 слева показано, как устанавливается разность расстояний точек А и В от плоскостей проекций π1, π2 и π3. Чертеж на рис. 44 справа дан с осями проекций.
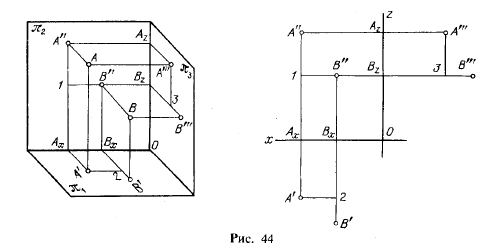
В данном примере разность расстояний точек от пл. π1 определяется отрезком А"l, равным А"Аx — В"Вx или А"'3, от пл. π2 — отрезком В'2, равным В'Вx — А'Аx или В"'3, от пл. π3 — отрезком В"l, равным A"Az — B"Bz или А'2.
ВОПРОСЫ К §§ 8 — 9
- Как образуются системы плоскостей проекций?
- Какому условию должна отвечать плоскость, вводимая в систему π1, π2 в качестве дополнительной плоскости проекций?
- Как строится проекция точки, заданной в еистеме π1, π2 на пл. π4, перпендикулярной к пл. π1?
- Устанавливаются ли расстояния точки от плоскостей проекций при наличии оси проекций?
- Как следует понимать чертеж точки при отсутствии оси проекций?
- Какое назначение имеют оси π4/π1 и π2/π5 на рис. 40 и 41?
- Как устанавливается на чертеже в системе π1, π2 расстояние точки от пл. π1, и от пл. π2?