Ортогональные проекции и система прямоугольных координат
ТеорияМодель положения точки в системе π1, π2, π3 (рис. 16) аналогична модели, которую можно построить, зная прямоугольные координаты 1) этой точки, т. е. числа, выражающие ее расстояния от трех взаимно перпендикулярных плоскостей — плоскостей координат. Прямые, по которым пересекаются плоскости координат, называются осями координат. Точка пересечения осей координат называется началом координат и обозначается буквой О2). Для осей координат будем применять обозначения, показанные на рис. 16.
Плоскости координат в своем пересечении образуют восемь трехгранных углов, деля пространство на восемь частей — восемь октантов 3). На рис. 16 изображен один из октантов. Показано образование отрезков, определяющих координаты некоторой точки А: из точки А проведены перпендикуляры к каждой из плоскостей координат.
1) Иначе — «декартовы координаты». Система координат Декарта может быть прямоугольной и косоугольной; здесь рассматривается прямоугольная система. Декарт (1596— 1650) — французский математик и философ.
2) Начальная буква латинского слова «origo» — начало.
3) Octo {лат.) — восемь.
Первая координата точки А, называемая ее абсциссой 1), выразится числом, полученным от сравнения отрезка АА'" (или равного ему отрезка ОАx на оси х) с некоторым отрезком, принятым за единицу масштаба. Также отрезок АА" (или равный ему отрезок 0Аy на оси у) определит вторую координату точки А, называемую ординатой 2); отрезок АА' (или равный ему отрезок 0Az на оси z) — третью координату, называемую аппликатой 3).
При буквенном обозначении координат абсцисса указывается буквой х, ордината — буквой у, аппликата — буквой z.
Построенный на рис. 16 параллелепипед называют параллелепипедом координат данной точки А. Построение точки по заданным ее координатам сводится к построению трех ребер параллелепипеда координат, составляющих трехзвенную ломаную линию (рис. 24). Надо отложить последовательно отрезки 0Аx, АxА' и А'А или 0Аy, А А'" и А"А и т. п., т. е. точку А можно получить шестью комбинациями, в каждой из которых должны быть все три координаты.
На рис. 24 для наглядного изображения взята известная из курса черчения средней школы проекция, называемая кабинетной 4). В ней оси х и z взаимно перпендикулярны, а ось у является продолжением биссектрисы угла xOz. В кабинетной проекции отрезки, откладываемые по оси у или параллельно ей, сокращаются вдвое.
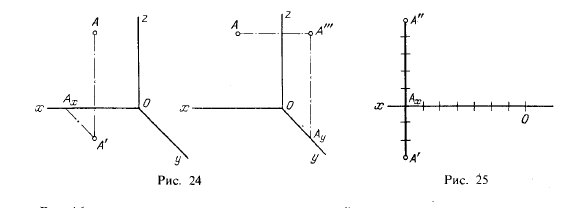
Рис. 16 показывает, что построение проекций точки сопровождается построением отрезков, определяющих координаты этой точки, если принять плоскости проекций за плоскости координат. Каждая из проекций точки А определяется двумя координатами этой точки; например, положение проекции А' определяется координатами х и у.
Положим, дана точка А (7; 3; 5); эта запись означает, что точка А определяется координатами x = 7, у = 3, z = 5. Если масштаб для построения чертежа задан или выбран, то (рис. 25) откладывают на оси х от некоторой точки О отрезок ОАx, равный 7 единицам, и на перпендикуляре к этой оси, проведенном из точки Аx, отрезки АxА' = 3 ед. и АxА" — 5 ед. Получаем проекции А' и А". Для построения достаточно взять только ось х.
Принимая оси проекций за оси координат, можно найти координаты точки по данным ее проекциям. Например, на рис. 18 отрезок ОАx выражает абсциссу точки А, отрезок АxА' — ее ординату, отрезок АxА" — аппликату.
Если задается лишь абсцисса, то этому соответствует плоскость, параллельная плоскости, определяемой осями у и z. Действительно, такая плоскость является геометрическим местом точек, у которых абсциссы равны заданной величине (рис. 26, плоскость ?).
1) Abscissa (лат.) — отсеченная, отделенная.
2) Ordinata (лат.) — от ordinatim ducta (лат.) — подряд проведенная.
3) Applicata (лат.) — приложенная.
4) Кабинетная проекция относится к числу косоугольных (подробнее см. в § 75).
Если задаются две координаты, то этим определяется прямая, параллельная соответствующей координатной оси. Например, имея заданными абсциссу и ординату, получаем прямую, параллельную оси z (на рис. 26 это прямая АВ). Она является линией пересечения двух плоскостей ? b ? где ? — геометрическое место точек с равными ординатами. Прямая АВ служит геометрическим местом точек, у которых равны между собой абсциссы и равны между собой ординаты.
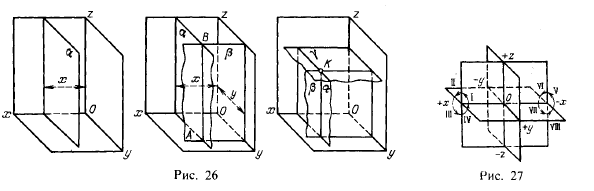
Если задаются все три координаты, то этим определяется точка. На рис. 26 показана точка К, полученная в пересечении трех плоскостей, из которых ? есть геометрическое место точек по заданной абсциссе, ? — по заданной ординате и у — по заданной аппликате.
Точка может находиться в любом из восьми октантов (нумерацию октантов см. на рис. 27). Следовательно, нужно знать не только расстояние данной точки от той или иной плоскости координат, но и направление, по которому надо это расстояние отложить; для этого координаты точек выражают относительными числами. Мы будем применять для отсчета координат систему знаков, указанную на рис. 27, т. е. будем применять систему координат, называемую «правой». Правая система характеризуется тем, что поворот на 90° «положительного» луча О (рис. 27) в сторону «положительного» луча Оy происходит против часовой стрелки (при условии, что мы смотрим на плоскость хОу сверху).
В системе, называемой «левой», «положительный» луч Ох направлен от точки О вправо.
При изображении тел обычно принимают в качестве плоскостей координат не плоскости проекций, а систему некоторых трех взаимно перпендикулярных плоскостей, непосредственно связанных с данным телом, например грани прямоугольного параллелепипеда, две грани и плоскость симметрии и т. п. Для такой системы координат встречается название «внутренняя».