Пересечение плоскостей

Теория

Использование универсального алгоритма для решения задач по определению линии пересечения поверхностей проследим вначале на наиболее простых примерах пересечения двух плоскостей.

Две плоскости пересекаются по прямой линии, для определения которой достаточно найти две точки, принадлежащие одновременно каждой из заданных плоскостей.

Чтобы найти такие точки, достаточно ввести две вспомогательные секущие плоскости γ1 и γ2 т. е. дважды выполнить последовательность операций, предусмотренных частью алгоритма (4), заключенной в квадратные скобки (см. § 43):

L1 = (γ1 ∩ α) ∩ (γ1 ∩ β);

L2 = (γ2 ∩ α) ∩ (γ2 ∩ β);

l = (L1, L2).

Рассмотрим общий случай пересечения плоскостей, когда обе плоскости - общего положения.

ПРИМЕР 1. Определить линию пересечения l плоскостей α(a ∩ b) и β(c || d) (рис. 183).

РЕШЕНИЕ. Проводим вспомогательную горизонтально проецирующую плоскость γ1(h0γ1). Определяем проекции прямых m1 = γ1 ∩ α и n1 = γ1 ∩ β. Так как плоскость γ1 | π1 , то m'1 и n'1 совпадут с h0γ1. С помощью точек 1', 2' и 3' 4' , принадлежащих прямым m'1 и n'1 определяем фронтальные проекции этих точек 1" , 2" и 3" , 4", которые определя прямые m"1 и n"1. Отмечаем точку пересечения фронтальных проекций прямых L"1 = m"1 ∩ n"1. Горизонтальная проекция L'1 принадлежит горизонтальным проекциям m'1 и n'1 .

Для нахождения точки L2 вводим плоскость γ2 || γ1 . Плоскость γ2 пересечет заданные плоскости по прямым m2 и n2, соответственно параллельным прямым m1 и n1 . Поэтому для определения их проекций достаточно найти проекции только одной точки, принадлежащей каждой из прямых m2 и n2 . На рис. 183

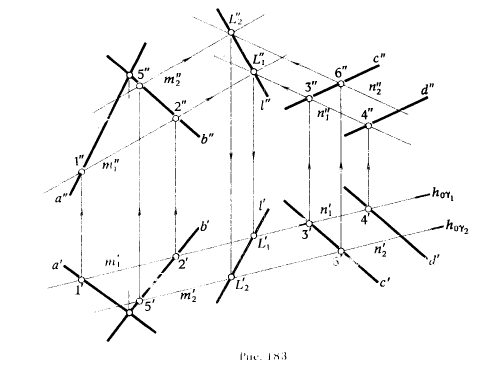
Рис 183.Пересечение плоскостей Рис 184-185.Пересечение плоскостей

за такие точки приняты 5 и 6. Пересечение m2 ∩ n2 = L2 . Точки L1 и L2 определяют искомую прямую l.

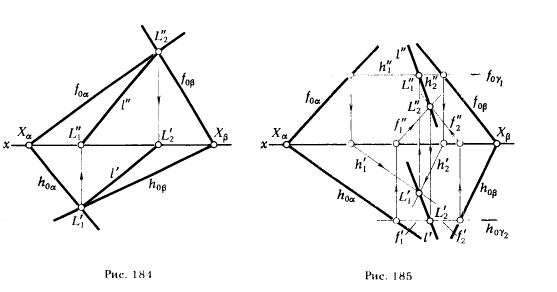
ПРИМЕР 2. Определить линию пересечения плоскостей α и β, заданных следами (рис. 184).

РЕШЕНИЕ. В данном случае решение значительно упрощается в связи с тем, что отпадает необходимость в выполнении построений, предусмотренных первым и вторым пунктами алгоритма (см.§ 43, табл. 8) . Это происходит потому, что роль вспомогательных секущих плоскостей γ1 и γ2 при задании плоскости следами могут выполнять плоскости проекций π1 и π2, а соответствующие следы h0α, h0β и f0α, f0β несут функции проекции прямых m' , n' и m" , n" . Следовательно, точки пересечения одноименных следов плоскостей α и β определяют положение проекций точек L1 и L2 .

L'1 = h0α ∩ h0β и L"2 = f0α ∩ f0β.-

Через одноименные проекции точек L1 и L2 проводим проекции искомой прямой l' и l".

Если одноименные следы плоскостей не пересекаются в пределах чертежа, то не представляется возможным использовать плоскости проекций в качестве вспомогательных секущих плоскостей. В этих случаях приходится вводить секущие плоскости, которые целесообразно проводить параллельно плоскостям проекций. Поясним сказанное на примере решения задачи по определению линии пересечения плоскостей α и β.

ПРИМЕР 3. Определить линию пересечения плоскостей α и β (рис. 185).

РЕШЕНИЕ. Вводим вспомогательные секущие плоскости γ1 || π1, и γ2 || π2. Эти плоскости пересекают заданные α и β по горизонталям h1 и h2 (плоскость γ1 ) и фронталям f1 и f2 (плоскость γ2 ) .

Находим точки L1 и L2: L'1 = h'1 ∩ h"2; L"2 = f"1 ∩ f"2. Зная L'1 и L"2, определяем L"1 и L'2. Через одноименные проекции точек L'1L'2 и L"1L"2 проводим проекции l' и l" искомой прямой пересечения плоскостей α и β.

Эту же задачу можно решить иначе. Вместо двух вспомогательных секущих плоскостей уровня взять одну плоскость γ общего положения, параллельную одной из заданных плоскостей α (или β) . Такой вариант решения основан на том что линии пересечения плоскости α двумя параллельными плоскостями β и γ параллельны между собой.

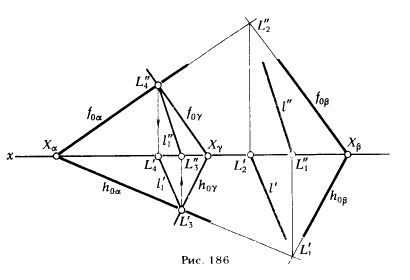
ПРИМЕР 4. Определить линию пересечения плоскостей α и β (рис. 186) .

РЕШЕНИЕ. Проводим вспомогательную секущую плоскость γ || β (h0γ || h0β и f0γ || f0β). Точку Хγ выбираем так, чтобы одноименные следы плоскостей α и γ пересекались в пределах чертежа. Находим l1 - линию пересечения плоскостей α и γ. Проекции l'1 и l"1 указывают направления проекций линии l пересечения плоскостей α и β.

Для определения точек, через которые пройдут эти проекции, рассмотрим ΔXαL"4Xγ ∼ ΔXαL"2Xβ В ΔXαL"4Xγ (L"4A"3) || (L"2L"1) ΔXαL"2Xβ, поэтому

Рис 186.Пересечение плоскостей Рис 187-188.Пересечение плоскостей Формула

Из этой пропорции определяем |ХαL"1| и через точку L"1 проводим l" || l"1.

Для нахождения горизонтальной про екции l' достаточно составить пропорцию:

Три отрезка из четырех заданы на чертеже, это дает возможность определить четвертый [ХαL'2]. Через точку L'2 проводим l'|| l'1 .

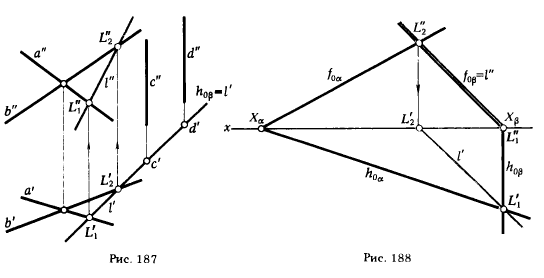
Решение задачи по определению линии пересечения плоскостей значительно упрощается, если одна из плоскостей занимает проецирующее положение. Из рис. 187 и 188 видно, насколько проще решается задача, когда одна из пересекающихся плоскостей - проецирующая, по сравнению с задачей (см. пример 1, рис. 183), в которой обе плоскости занимают общее положение. В этих случаях появляется возможность воспользоваться инвариантом (Ф ⊂ β)∧(β ⊥ π1 ) ⇒ Ф' ⊂ h0β, поэтому одна из проекций линии пересечения (l' на рис. 187 и l" на рис. 188) входит в состав исходных данных задачи (l' ≡ h0β на рис. 187 и l" ≡ f0β на рис. 188). Решение сводится к определению недостающей проекции прямой, принадлежащей плоскости (см. § 41, пример 2, рис. 179).