Плоскость, касательная к поверхности
ТеорияКасательные плоскости играют большую роль в геометрии. Построение касательных плоскостей в практическом отношении имеет важное значение, так как наличие их позволяет определить направление нормали к поверхности в точке касания. Эта задача находит широкое применение в инженерной практике. К помощи касательных плоскостей обращаются также для построения очерков геометрических фигур, ограниченных замкнутыми поверхностями. В теоретическом плане плоскости, касательные к поверхности, используются в дифференциальной геометрии при изучении свойств поверхности в районе точки касания.
Основные понятия и определения
Плоскость, касательную к поверхности, следует рассматривать как предельное положение секущей плоскости (по аналогии с прямой, касательной к кривой, которая также определяется как предельное положение секущей).
Плоскость, касательная к поверхности в заданной на поверхности точке, есть множество всех прямых - касательных, проведенных к поверхности через заданную точку.
В дифференциальной геометрии доказывается, что псе касательные к поверхности, проведенные в обыкновенной точке, компланарны (принадлежат одной плоскости).
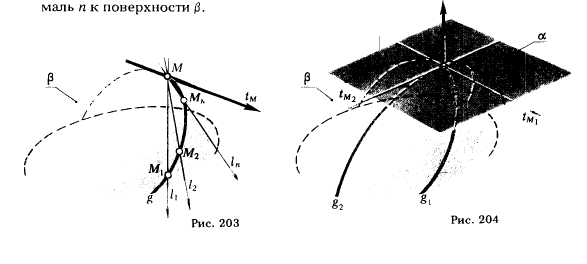
Выясним, как проводится прямая, касательная к поверхности. Касательная t к поверхности β в заданной на поверхности точке М (рис. 203) представляет предельное положение секущей lj, пересекающей поверхность в двух точках (ММ1, ММ2, ..., ММn), когда точки пересечения совпадают (М ≡ Мn, ln ≡ lM). Очевидно {M1, М2, ..., Мn} ∈ g, так как g ⊂ β. Из сказанного выше вытекает следующее определение: касательной к поверхности называется прямая, касательная к какой-либо кривой, принадлежащей поверхности.
Так как плоскость определяется двумя пересекающимися прямыми, то для задания плоскости, касательной к поверхности в заданной точке, достаточно провести через эту точку две произвольные линии, принадлежащие поверхности (желательно простые по форме), и к каждой из них построить касательные в точке пересечения этих линий. Построенные касательные однозначно определяют касательную плоскость. Наглядное представление о проведении плоскости α, касательной к поверхности β в заданной точке М, дает рис. 204. На этом рисунке показана также нормаль n к поверхности β.
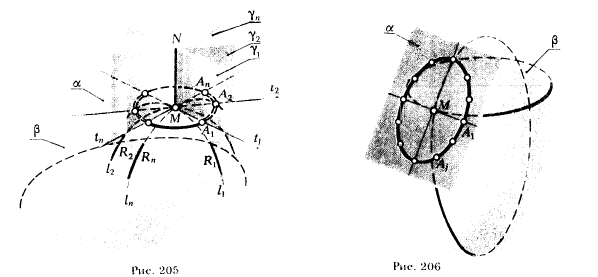
Нормлью к поверхности в заданной точке называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.
Линию пересечении поверхности плоскостью, проходящей через нормаль, называют нормальным сечением поверхности. В зависимости от вида поверхности касательная плоскость может иметь, с поверхностью как одну, так и множество точек (линию). Линия касания может быть в то же время и линией пересечения поверхности с плоскостью.
Возможны также случаи, когда на поверхности имеются точки, на которых невозможно провести касательную к поверхности; такие точки называют особыми. В качестве примера особых точек можно привести точки, принадлежащие ребру возврата торсовой поверхности, или точку пересечения меридиана поверхности вращения с ее осью, если меридиан и ось пересекаются не под прямым углом.
Виды касания зависят от характера кривизны поверхности.
Кривизна поверхности
Вопросы кривизны поверхности были исследованы французским математиком Ф. Дюпеном (1784- 1873), который предложил наглядный способ изображения изменения кривизны нормальных сечений поверхности.
Для этого в плоскости, касательной к рассматриваемой поверхности в точке М (рис. 205, 206), на касательных к нормальным сечениям по обе стороны от данной точки откладываются отрезки, равные корням квадратным из величин соответствующих радиусов кривизны этих сечений. Множество точек - концов отрезков задают кривую, называемую индикатрисой Дюпена. Алгоритм построения индикатрисы Дюпена (рис. 205) можно записать:
1. M ∈ α, M ∈ β ∧ α 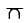 β;
β;
2. [MN) ⊥ α, [MN) ⊥ β;
3. [MN) ⊂ γ1, [MN) ⊂ γ2,...,[MN) ⊂ γn;
4. γ1 ∩ β = t1,γ2 ∩ β = t2,...,γn ∩ β = tn
5. γ1 ∩ α = t1,γ2 ∩ α = t2,...,γn ∩ α = tn
6. [MA1] = √(Rl1),[MA2] = √(Rl2),...,[MAn] = √(Rln)
где R - радиус кривизны.
(A1 ∪ А2 ∪ ... ∪ Аn) - индикатриса Дюпена.
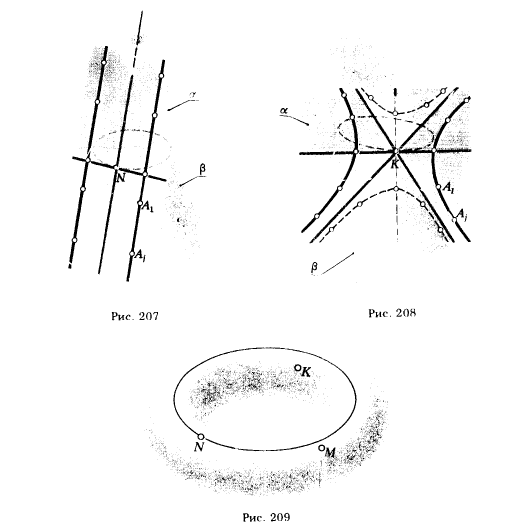
Если индикатриса Дюпена поверхности - эллипс, то точка М называется эллиптической, а поверхность - поверхностью с эллиптическими точками (рис. 206). В этом случае касательная плоскость имеет с поверхностью только одну общую точку, а все линии, принадлежащие поверхности и пересекающиеся в рассматриваемой точке, расположены по одну сторону от касательной плоскости. Примером поверхностей с эллиптическими точками могут служить: параболоид вращения, эллипсоид вращения, сфера (в этом случае индикатриса Дюпена - окружность и др.).
При проведении касательной плоскости к торсовой поверхности плоскость будет касаться этой поверхности по прямой образующей. Точки этой прямой называются параболическими, а поверхность - поверхностью с параболическими точками. Индикатриса Дюпена в этом случае - две параллельные прямые (рис. 207*).
На рис. 208 показана поверхность, состоящая из точек, в кото
* Кривая второго порядка - парабола - при определенных условиях может распадаться на две действительные параллельные прямые, две мнимые параллельные прямые, две совпадающие прямые. На рис. 207 мы имеем дело с двумя действительными параллельными прямыми.
рых касательная плоскость пересекает поверхность. Такая поверхность называется гиперболической, а принадлежащие ей точки - гиперболическими точками. Индикатриса Дюпена в данном случае - гипербола.
Поверхность, все точки которой являются гиперболическими, имеет форму седла (косая плоскость, однополостный гиперболоид, вогнутые поверхности вращения и др.).
Одна поверхность может иметь точки разных видов, например, у торсовой поверхности (рис. 209) точка М эллиптическая; точка N - параболическая; точка К - гиперболическая.
В курсе дифференциальной геометрии доказывается, что нормальные сечения, в которых величины кривизны Kj = 1/ Rj (где Rj радиус кривизны рассматриваемого сечения) имеют экстремальные значения, расположены в двух взаимно перпендикулярных плоскостях.
Такие кривизны К1 = 1/Rmax. К2 = 1/Rmin называются главными, а значения Н = (К1 + К2)/2 и К = К1К2 - соответственно средней кривизной поверхности и полной (гауссовой) кривизной поверхности в рассматриваемой точке. Для эллиптических точек К > 0, гиперболических К < 0, параболических К = 0.
Задание плоскости касательной к поверхности на эпюре Монжа
Ниже на конкретных примерах покажем построение плоскости, касательной к поверхности с эллиптическими (пример 1), параболическими (пример 2) и гиперболическими (пример 3) точками.
ПРИМЕР 1. Построить плоскость α, касательную к поверхности вращения β, с эллиптическими точками. Рассмотрим два варианта решения этой задачи, а) точка М ∈ β и б) точка М ∉ β
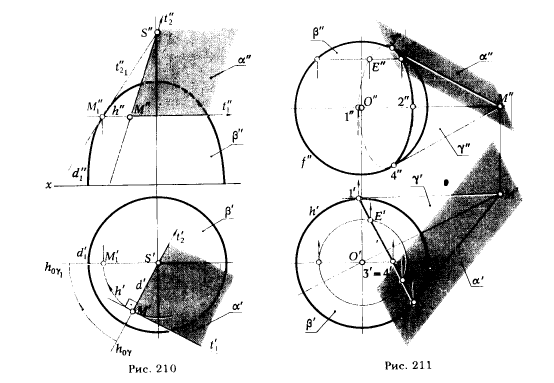
Вариант а (рис. 210).
Касательная плоскость определяется двумя касательными t1 и t2, проведенными в точке М к параллели и меридиану поверхности β.
Проекции касательной t1 к параллели h поверхности β будут t'1 ⊥ (S'M') и t"1 || оси х. Горизонтальная проекция касательной t'2 к меридиану d поверхности β, проходящему через точку М, совпадет с горизонтальной проекцией меридиана. Чтобы найти фронтальную проекцию касательной t"2, меридиональную плоскость γ(γ ∋ М) путем вращения вокруг оси поверхности β переводим в положение γ1, параллельное плоскости π2. В этом случае точка М → M1(М'1 , М"1).Проекция касательной t"2 rarr; t"21 определяется (M"1S"). Если мы теперь возвратим плоскость γ 1 в первоначальное положение, то точка S" останется на месте (как принадлежащая оси вращения), а М"1 → М" и фронтальная проекция касательной t"2 определится (M"S")
Две пересекающиеся в точке М ∈ β касательные t1 и t2 определяют плоскость α, касательную к поверхности β.
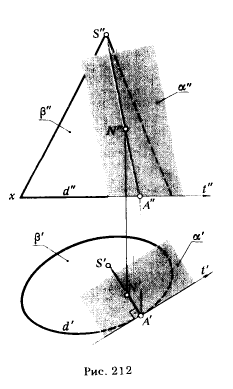
Вариант б (рис. 211)
Для построения плоскости, касательной к поверхности проходящей через точку, не принадлежащую поверхности, нужно исходить из следующих соображений: через точку вне поверхности, состоящей из эллиптических точек, можно провести множество плоскостей, касательных к поверхности. Огибающей этих поверхностей будет некоторая коническая поверхность. Поэтому, если нет дополнительных указаний, то задача имеет множество решений и в таком случае сводится к проведению конической поверхности γ, касательной к данной поверхности β.
На рис. 211 показано построение конической поверхности γ, касательной к сфере β. Любая плоскость α, касательная к конической поверхности γ, будет касательной к поверхности β.
Для построения проекций поверхности γ из точек М' и М" проводим касательные к окружностям h' и f" - проекциям сферы. Отмечаем точки касания 1 (1' и 1"), 2 (2' и 2"), 3 (3' и 3") и 4 (4' и 4"). Горизонтальная проекция окружности - линия касания конической поверхности и сферы спроецируется в [ 1'2'] Для нахождения точек эллипса, в который эта окружность спроецируется на фронтальную плоскость проекций, воспользуемся параллелями сферы.
На рис. 211 таким способом определены фронтальные проекции точек Е и F (Е" и F"). Имея коническую поверхность γ, строим к ней касательную плоскость α. Характер и последовательность графичес-
ких построений, которые необходимо для этого выполнить, приведены в следующем примере.
ПРИМЕР 2 Построить плоскость α, касательную к поверхности β с параболическими точками
Как в примере 1 рассмотрим два варианта решения .а) точка N ∈ β; б) точка N ∉ β
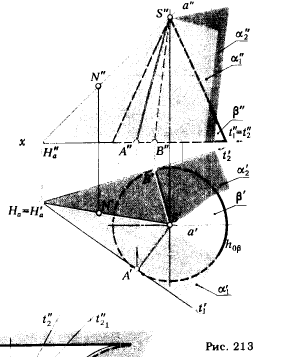
Вариант а ( рис 212) .
Коническая поверхность относится к поверхностям с параболическими точками (см. рис. 207.) Плоскость, касательная к конической поверхности, касается ее по прямолинейной образующёи.Для ее построения необходимо:
1) через данную точку N провести образующую SN (S'N' и S"N") ;
2) отметить точку пересечения образующей (SN) с направляющей d: (SN) ∩ d = А;
3) провеет и к асательную t к d в точке А.
Образующая (SA) и пересекающая ее касательная t определяютплоскостъ α , касательную к конической поверхности β в данной точке N*.
Для проведения плоскости α, касательной к конической поверхности β и проходящей через точку N, не принадле
* Так как поверхность β состоит из параболических точек (кроме вершины S), то касательная к ней плоскость α будет иметь общую с ней не одну точку N, а прямую (SN).
жащую заданной поверхности, необходимо:
1) через данную точку N и вершину S конической поверхности β провести прямую а (а' и а") ;
2) определить горизонтальный след этой прямой Нa;
3) через Нa провести касательные t'1 и t'2 кривой h0β - горизонтальному следу конической поверхности;
4) точки касания А (А' и А") и В (В' и В") соединить с вершиной конической поверхности S (S' и S").
Пересекающиеся прямые t1, (AS) и t2, (BS) определяют искомые касательные плоскости α1 и α2
ПРИМЕР 3. Построить плоскость α, касательную к поверхности β с гиперболическими точками.
Точка К (рис. 214) находится на поверхности глобоида (внутренняя поверхность кольца).
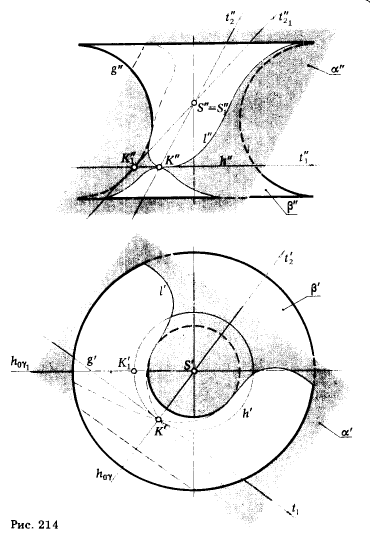
Для определения положения касательной плоскости α необходимо:
1) провести через точку К параллель поверхности β h(h', h") ;
2) через точку К' провести касательную t'1 ( t"1 ≡ h" ) ;
3) для определения направлений проекций касательной к меридиональному сечению необходимо провести через точку К и ось поверхности плоскость γ, горизонтальная проекция t'2 совпадет с h0γ; для построения фронтальной проекции касательной t"2 предварительно переведем плоскость γ путем вращения ее вокруг оси поверхности вращения в положение γ1 || π2. В этом случае меридиональное сечение плоскостью γ совместится с левой очерковой дугой фронтальной проекции - полуокружностью g".
Точка К (К', К"), принадлежащая кривой меридионального сечения, переместится в положение K1 (К'1, К"1). Через К"1 проводим фронтальную проекцию касательной t"21, в совмещенном с плоскостью γ1 || π2 положении и отмечаем точку ее пересечения с фронтальной проекцией оси вращения S"1. Возвращаем плоскость γ1 в исходное положение, точка К"1 → К" (точка S"1 ≡ S"). Фронтальная проекция касательной t"2 определится точками К" и S".
Касательные t1 и t2 определяют искомую касательную плоскость α, которая пересекает поверхность β по кривой l .
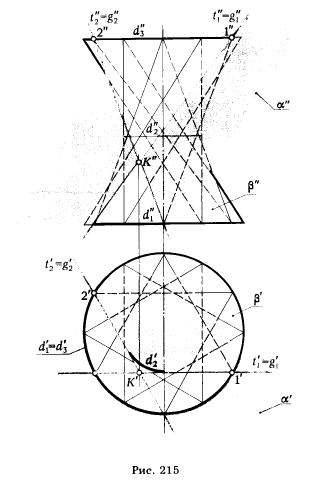
ПРИМЕР 4. Построить плоскость α, касательную к поверхности β в точке К. Точка К находится на поверхности однополостного гиперболоида вращения (рис. 215).
Эту задачу можно решить, придерживаясь алгоритма, использованного в предыдущем примере, но учитывая, что поверхность однополостного гиперболоида вращения является линейчатой поверхностью, которая имеет два семейства прямолинейных образующих, причем каждая из образующих одного семейства пересекает все образующие другого семейства (см. § 32, рис. 138). Через каждую точку этой поверхности можно провести две пересекающиеся прямые - образующие, которые будут одновременно касательными к поверхности однополостного гиперболоида вращения.
Эти касательные определяют касательную плоскость, т е. плоскость, касательная к поверхности однополостного гиперболоида вращения ,пересекает эту поверхность по двум прямым g1 и g2. Для построения проекций этих прямых достаточно ит горизонтальной проекции точки К пронести касательные t'1 и t'2 к горизон-
тальной проекции окружности d'2 - горла поверхности однополостного гиперболоида вращения; определить точки 1' и 2 , в которых t'1 и t'2 пересекают одну ит направляющих поверхности d1 . По 1' и 2' находим 1" и 2" , которые совместно с К" определяют фронтальные проекции искомых прямых.