Пересечение поверхности плоскостью (построение сечения)

При пересечении поверхности или какой-либо геометрической фигуры плоскостью получается плоская фигура, которую называют сечением.

Сечение поверхности плоскостью в общем случае представляет собой кривую (или прямую, если пересекаются плоскости), принадлежащую секущей плоскости.

Определение проекций линий сечения следует начинать с построения опорных точек - точек, расположенных на очерковых образующих поверхности (точки, определяющие границы видимости проекций кривой); точек, удаленных на экстремальные (максимальное и минимальное) расстояния от плоскостей проекций. После этого определяют произвольные точки линии сечения.

Если произвольные точки определяются с помощью одного и того же приема, то для нахождения опорных точек, как правило, приходится пользоваться различными способами.

В дальнейшем при построении сечения поверхности и линии пересечения поверхностей будет показано нахождение как опорных так и произвольных точек сечения.

А. Построение сечения многогранников.

Многогранником называют пространственную фигуру, ограниченную замкнутой поверхностью, состоящей из отсеков плоскостей, имеющих форму многоугольников (в частном случае треугольников).

Стороны многоугольников образуют ребра, а плоскости многоугольников - грани многогранника.

Проекциями сечения многогранников, в общем случае, являются многоугольники, вершины которых принадлежат ребрам, а стороны - граням многогранника*. Поэтому задачу по определению сечения многогранника можно свести к многократному решению задачи по определению точки встречи прямой (ребер многогранника) с плоскостью или к задаче по нахождению линии пересечения двух плоскостей (грани многогранника и секущей плоскости).

Первый путь решения называют способом ребер, второй - способом граней. Какому из способов следует отдать предпочтенение, надо решать в каждом конкретном случае.

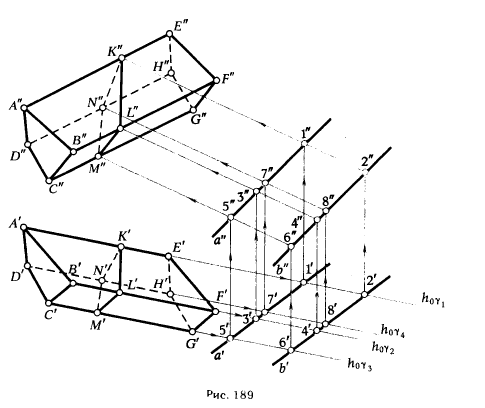
ПРИМЕР 1. Определить сечение четырехгранной призмы ABCDEFGH (рис. 189) плоскостью α(а || b).

РЕШЕНИЕ. Решаем эту задачу способом ребер. Для этого заключаем ребра в горизонтально проецирующие плоскости γ₁, γ₂, γ₃, γ₄: γ₁ ⊃ (АЕ); γ₂ ⊃ (BF); γ₃ ⊃ (CG); γ₄ ⊃ (DH).

Находим проекции линий пересечения этих плоскостей с плоскостью α (прямые 1, 2; 3, 4; 5, 6; 7, 8). Отмечаем точки пересечения полученных прямых с соответствующими ребрами призмы К = (1, 2) ∩ (АЕ); L = (3, 4) ∩ (BF); М = (5, 6) ∩ (CG); N= (7,8) ∩ (DH). Четырехугольник KLMN - искомое сечение.

Решение задачи значительно упрощается, если секущая плоскость или плоскости граней (если многогранник относится к призмам) занимает проецирующее положение.

ПРИМЕР 2. Определить сечение трехгранной пирамиды SABC горизонтально проецирующей плоскостью α (рис. 190).

Для получения ответа на посталвенную задачу не требуется никаких дополнительных построений. На основании инвариантного свойства 2г (§ 6) горизонтальная проекция сечения пирамиды плоскостью а должна принадлежать следу плоскости h_0α. Поэтому достаточно отметить точки М' , N', L', в которых горизонтальный след h_0α секущей плоскос-

* В частном случае многоугольник сечения может проецироваться в отрезок прямой (см. инвариантное свойство 2г, § 6).

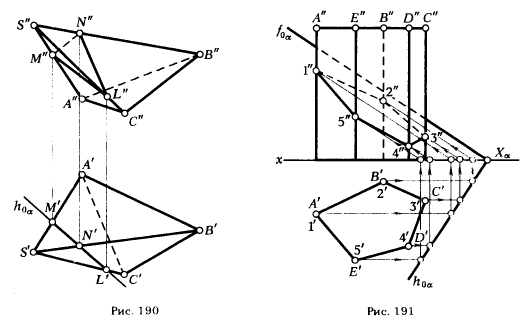
ти α пересекает горизонтальные проекции ребер пирамиды.

Фронтальные проекции вершин треугольника сечения определяются по их горизонтальным проекциям. Для этого достаточно из точек М', N', L' провести линии связи - вертикальные прямые и отметить точки их пересечения с фронтальными проекциями ребер пирамиды.

ПРИМЕР 3. Определить сечение пятигранной призмы ABCDE, ребра которой перепендикулярны горизонтальной плоскости проекции, секущая плоскость α - общего положения (рис. 191).

Так как ребра призмы перпендикулярны плоскости π₁, то горизонтальные проекции точек пересечения этих ребер с плоскостью α(1', 2', 3', 4', 5') совпадают с горизонтальными проекциями ребер, т. е. точками А', В', С, D', Е'.

Фронтальные проекции точек встречи определяем из условия принадлежности этих точек плоскости α. Решение сводится к нахождению недостающей проекции точки, принадлежащей плоскости, если известна хотя бы одна из ее проекций (см. §40, пример 3, рис. 171). На рис. 191 фронтальные проекции точек 1", 2", 3", 4", 5" найдены с помощью фронтальной плоскости α.

Б. Построение сечения поверхности вращения.

Так как для рассматриваемого круга задач в алгоритме l = (L₁ ∪ L₂ ∪ L₃ ∪ ... ∪ L_n); [L_j = (γ_j ∩ α) ∩ (γ_j ∩ β) ] α - поверхность вращения, а β - плоскость, то для нахождения общих точек L_j, ... , принадлежащих как поверхности α, так и плоскости β, целесообразно в качестве вспомогательных секущих поверхностей γ_j принять плоскости, перпендикулярные к оси вращения; в этом случае плоскости γ_j будут пересекать поверхность α по окружностям, а плоскость β по линиям уровня *. Определение точек L_j сводится к нахождению точек пересечения прямой с окружностью.

ПРИМЕР. Определить сечения поверхности сферы а плоскостью общего положения β (рис. 192).

РЕШЕНИЕ. При сечении поверхности сферы плоскостью получается окружность. Если секущая плоскость общего положения, то эта окружность проецируется на плоскости проекций в виде эллипсов.

Построения начнем с определения опорных точек. Для нахождения низшей А и высшей В точки кривой сечения проводим через центр сферы О вспомогательную секущую плоскость γ₁ ⊥ h_0β. Точки А и В принадлежат линии пересечения плоскостей γ₁ и β. Эти точки находят в результате пересечения прямой (1, 2) = γ₁ ∩ β с поверхностью α. А и В = (1, 2) ∩ α. Для их определения воспользуемся способом замены плоскостей проекции. Перейдем от системы xπ₂/π₁ к x₁π₃/π₁. Ось x₁ проводим перпендикулярно h_0β. По отношению к π₃ плоскость β занимает проецирующее положение, поэтому точки А"₁ и В"₁, в которых след f_0β1, пересекает новую фронтальную проекцию очерка сферы α"₁, будут вспомогательными проекциями искомых точек. Обратными построениями определяем положение горизонтальных А', В', а затем и фронтальных А". В" проекций искомых точек.

[А'В'] является малой осью (диаметром) горизонтальной проекции эллипса. Для определения большого диаметра этого эллипса [ D' Е' ] достаточно из вспомогательной проекции центра сферы

О"₁ провести прямую, перпендикулярную к отрезку [А"₁В"₁]. Точка С"₁(С', С"), в которой перпендикуляр пересекает [A"₁, В"₁], является центром эллипса, через который пройдет сопряженный (большой) диаметр эллипса DE.

DE принадлежит горизонтали плоскости β. Для определения точек D и Е вводим вспомогательную секущую плоскость γ₂, проходящую через точку С и параллельную плоскости проекций π₁. Эта плоскость пересекает поверхность сферы по окружности с, которая проецируется на плоскость π₁ без искажения в окружность радиуса R = [ 6" 7"], проведенную из центра О'. Пересечение этой окружности с горизонтальной проекцией горизонтали h₂ определяет положение горизонтальных проекций точек D' и Е'. Для нахождения точек F и G, являющихся граничными точками видимости для фронтальной проекции эллипса, воспользуемся плоскостью γ₃ || π₂ . Эта плоскость пересечет поверхность сферы по главному меридиану, который проецируется на π₂ во фронтальную проекцию очерка сферы, а плоскость β по фронтали f₃ (f'₃ f"₃ ). Пересечение f"₃ с фронтальной проекции очерка сферы укажет положение точек F" и G".

Для нахождения точек М и N, указывающих границы видимости на горизонтальной проекции сечения, проводим плоскость γ₄ || π₁ (γ₄ ∋ О).

Плоскость γ₄ ∩ β = h₄ , а поверхность сферы - по окружности, которая проецируется на плоскость π₁ в горизонтальную проекцию очерка сферы.

* Имеется в виду, что ось поверхности вращения перпендикулярна плоскости проекции.

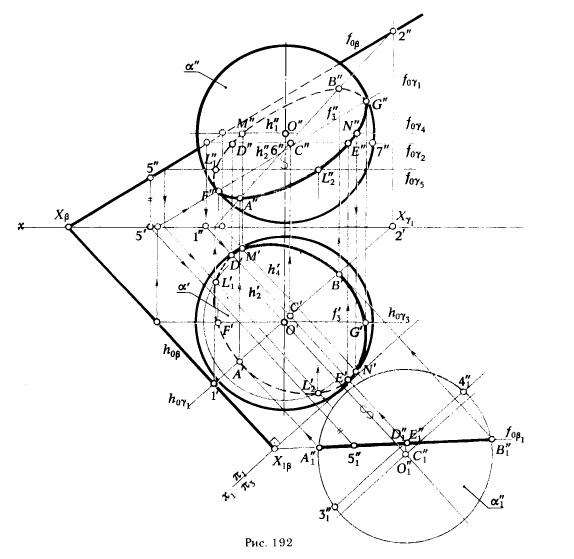
Пересечение h'₄ с горизонтальным очерком сферы α' определяет положение искомых горизонтальных проекций точек M' и N'

Для определения произвольных точек L₁ и L₂, принадлежащих линии сечения, как правило, целесообразно в качество вспомогательной секущей плоскости использовать плоскости уровня

На рис 192 показано построение точек L₁ и L₂ , с помощью горизонтальной плоскости γ₅. Проведя плоскости γ_j || π₁ мы каждый раз будем получать окружность в результате пересечения γ_j с α и прямую - горизонталь при пересечении γ_j с β. Пересечения окружностей и прямых укажут положение горизонтальных проекций точек , принадлежащих горизонтальной проекции линии сечения

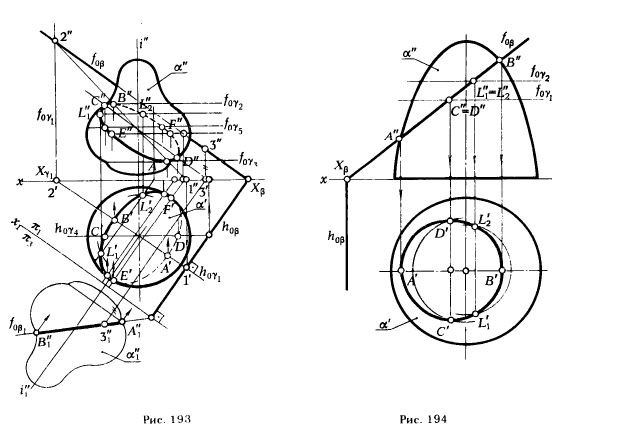
Если задана произвольная поверхность вращения, то ход решения задачи и последовательность выполнения геометрических построении ничем не отличается от случая, рассмотренного на рис. 192.

На рис. 193 показано построение сечения произвольной поверхности вращения α плоскостью общего положения β. Как и в предыдущем примере, вначале определены опорные точки: низшая A и высшая B: точки С, I) - границы видимости на фронтальной и точки Е. F - на горизонтальной проекциях. На рис. 193 показано также построение произвольных точек L₁ и L₂.

Решение задачи но определению сечения поверхности вращения α плоскостью значительно упрощается, если секущая плоскость занимает проецирующее положение. В этом случае одна из проекций сечения - отрезок примой, принадлежит следу плоскости.

Задача по определению второй проекции линии сечения сводится к многократному решению ранее рассмотренной задачи по нахождению второй проекции точки, принадлежащей плоскости, если известна хотя бы одна ее проекции (см. § 40, пример 3, рис. 171).

Рис. 194 дает представление о таком частном случае решения задачи. Из чертежа видно, что оно проще решении, рассмотренных на рис:. 192 и 193. Потому целесообразно при решении задач на определение сечения поверхности плоскостью предварительно перевести секущую плоскость в проецирующее положение.

В. Построение сечения поверхности прямого кругового конуса.

Поверхность прямого кругового конуса относится к поверхностям вращения, но мы рассматриваем ее отдельно, гак как она занимает особое место среди других поверхностей вращения. Эта поверхность н своем роде уникальна, она служит носителем замечательных кривых второго порядка: окружности, зллипса, параболы и гиперболы. Роль и области использования лих кривых в науке и, особенно, технике невозможно переоценить.

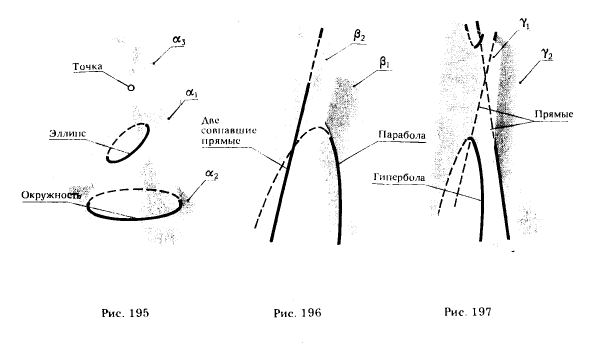
Все перечисленные кривые являются плоскими и, следовательно, могут быть получены в результате сечения конической поверхности плоскостью. В связи с этим перечисленные кривые называют также коническими сечениями. В частных случаях при определенном положении секущих плоскостей α₃, β₂, γ₁, (см. рис. 195, 196, 197) кривые

второго порядка распадаются на две прямые (действительные или мнимые *).

Прежде чем говорить о построении ортогональных проекций сечения поверхности прямого кругового конуса, отметим существование теоремы, которой будем пользоваться при построении кривых второго порядка.

Т е о р е м а: ортогональная проекция плоского сечения поверхности прямого конуса на плоскость, перпендикулярную к его оси, представляет собой кривую второго порядка и имеет одним из своих фокусов ортогональную проекцию на эту плоскость вершины конической поверхности.

Условия, которые должны быть выполнены, чтобы получить ту или иную кривую второго порядка, при сечении конической поверхности плоскостью могут быть установлены из свойств кривых второго порядка.

Известно, что эллипс представляет кривую второго порядка, не имеющую бесконечно удаленных (несобственных) точек. Поэтому, чтобы получить в сечении конической поверхности эллипс, надо выбрать такую плоскость, которая пересекает все прямолинейные образующие этой поверхности. В частном случае, когда диаметры эллипса равны (секущая плоскость перпендикулярна к оси конической поверхности) , в сечении получается окружность.

Из аффинной геометрии известно, что параболой называется кривая второго порядка, касающаяся несобственной прямой, или, что то же самое, кривая, имеющая одну несобственную точку. В связи с этим для получения параболы необходимо, чтобы секущая плоскость была параллельно одной образующей конической поверхности. В пределе, когда секущая плоскость переходит в касательную к поверхности, две симметричные дуги параболы преобразуются в две полупрямые, принадлежащие одной прямой.

* Плоскость α₃ (рис. 195) пересекает коническую поверхность по двум мнимым прямым, пересекающимся в собственной точке.

И, наконец, гипербола с аффинной точки прения представляет собой кривую второго порядка, пересекающую несобственную прямую, или, иначе, гипербола - кривая второго порядка, имеющая две несобственные точки, т. е. чтобы получить гиперболу, нужно секущую плоскость взять параллельной двум прямолинейным образующим. В частном случае, когда секущая плоскость проходит через вершину конической поверхности, гипербола распадается на две пересекающиеся прямые.

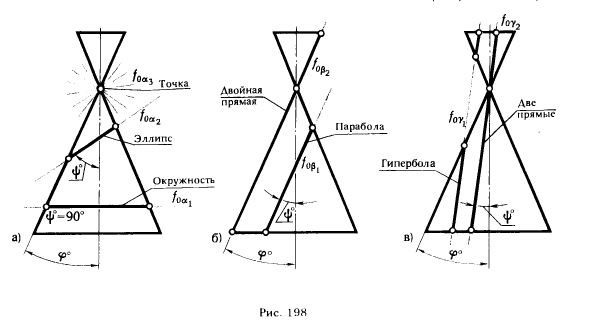
На рис. 195 показаны положение секущей плоскости для получения эллипса (плоскость α₁ ) и окружности (плоскость α₂) и одна из плоскостей, принадлежащих связке, проходящей через вершину конической поверхности, и пересекающих эту поверхность по двум мнимым прямым, пересекающимся в действительной точке (плоскость α₃) . На рис. 196 показаны положение секущей плоскости для получения параболы (плоскость β₁ ) и плоскость β₂, имеющая с конической поверхностью общую прямую (точнее две совпавшие прямые). На рис. 197 изображены плоскость γ₁ , пересекающая коническую поверхность по гиперболе, и плоскость γ₂, в сечении которой образуются две пересекающиеся прямые.

На рис. 198 приведены фронтальные проекции поверхности прямого кругового конуса, следы фронтально проецирующих секущих плоскостей и указан вид получаемой в сечении кривой. По рис. 198 можно установить признаки, обеспечивающие получение в сечении той или иной кривой второго порядка. Так, если обозначить угол наклона образующей конической поверхности к его оси через φ°, а угол между секущей плоскостью и той же осью через ψ°, то можно утверждать, что при > (рис. 198,а) в сечении получается эллипс (в частном случае, если ψ° = 90°, окружность), при 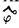= 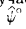(рис. 198, .б) - парабола и при 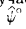< 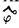(рис. 198,в) - гипербола.

Проследим па примерах характер графических построений, которые должны быть выполнены для построения сечения поверхности прямою кругового конуса.

ПРИМЕР 1. Построить проекции сечения поверхности прямого кругового конуса ω плоскостью α (рис. 199)

РЕШЕНИЕ. Плоскость α фронтально проецирующая. Угол между секущем плоскостью и осью конической поверхности ψ° больше угла наклона образующей конической поверхности к его оси, поэтому в сечении получим эллипс, большая ось которого [AB] будет проецироваться на плоскость π₂ без искажения в [A"B"], а малая ось эллипса CD спроецируется на плоскость π₂ в точку С" D", расположенную в середине оотрезка [A"B"]. Величина мамой оси [CD] определяется на условия (C, D) ∈ α. Проводим через С"D" фрональную проекцию параллели поверхности α - h". Дли построении ее горизтотальной проекции из горизонтальной проекции фокуса эллипса S' проводим окружность радиусом |1"2"| и отмечаем точки ее пересечени С" и D" с перпендикуляром, востановленным в середине |A'B'| - горизонтальной проекции большой оси эллипса. Зная большой и малый диаметры эллипса, известным способом строим эллипс.

ПРИМЕР 2. На рис. 200 показаны проекции поверхности прямого кругоного конуса ω и фрнтально проецирующей плоскости β. Построить проекции липни сечении.

РЕШЕНИЕ. Угол наклона секущей плоскости β к оси конической понерхности ранен yглу наклона прямолинейной образующей к этой оси 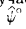. Потому в сечении получится парабола, вершина которой спроецируется в точку А (А', A"), а горизонтальная проекция фокуса в точку S', проводим директрису параболы. По данным директрисе и фокусу строим параболу. Фронтальная проекция дуги параболы проецируется в [A"B"] совпадающей с f_0β

ПРИМЕР 3.Построить проекции сечения поверхности прямого кругового конуса ω плоскостью γ (рис 20 I).

РЕШЕНИЕ. Так как / ψ° наклона секу щей плоскости γ к оси конической поверхности меньше угла наклона образущей конической поверхности / φ°, то плоскость γ пересечет поверхность ω по гиперболе. Фокусы и вершины горизонтальной проекции ее ветвей определяются непосредственно из чертежа .С помощью фокусов и вершин строим асимптоты горизонтальной проекции гиперболы. Зная положение вершин, фокусов и асимптот, можно построить любое число точек, принадлежащих ветвям гиперболы

В рассмотренных примерах пересекающая коническую поверхность плоскость занимала проецирующее положение. Если секущая плоскость общего положения, то целесообразно с помощью способов преобразования перевести ее в проецирующее положение. Это позволит свести задачу к простейшей - одному из рассмотренных случаев (рис. 199 ... 201).

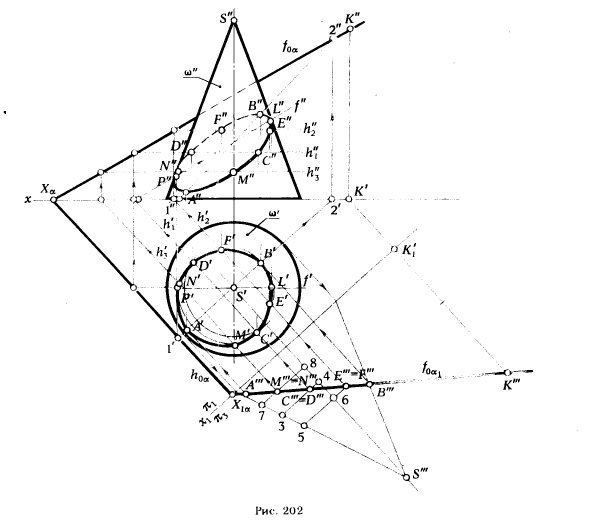
ПРИМЕР 4. Построить проекции сечения конической поверхности ω плоскостью α (рис. 202).

РЕШЕНИЕ. Чтобы упростить решение задачи, осуществим замену плоскости π₂ новой плоскостью π₃. Плоскость π₃ выбираем так, чтобы по отношению к ней секущая плоскость α заняла проецирующее положение. Спроецируем на плоскость π₃ коническую поверхность ω. Выполненные преобразования позволили свести решение к случаю, рассмотренному ранее (см. пример 1, рис. 199) .

Для построения фронтальной проекции зллипса сечения на рис. 202, кроме точек А, В и С, D, на вспомогательной проекции взяты точки Е, F и М, N, горизонтальные и фронтальные проекции этих точек определены с помощью горизонталей h₂ и h₃. Кроме опорных точек А и В, являющихся высшей (B) и низшей (A) точками сечения, на рис. 202 показаны точки Р и L, принадлежащие фронтальным проекциям очерковых образуещих конической поверхности ω. Эти точки служат границей видимости для фронтальной проекции сечения. Для нахождения точек Р" и L" пользуемся фронталью f.