Построение линии пересечения поверхностей с помощью семейства вспомогательных сферических поверхностей

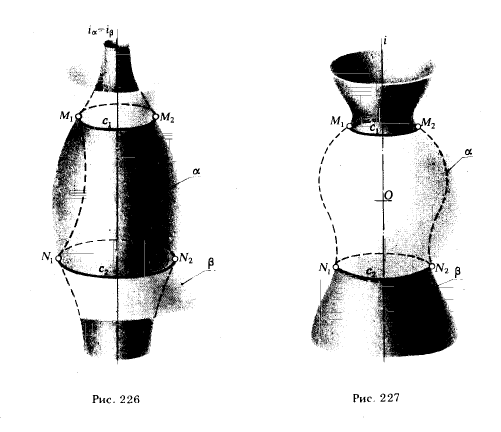
Для определения линии пересечения двух произвольных поверхностей вращения целесообразно воспользоваться одним свойством, присущим поверхностям вращения, которое состоит в том, что две любые соосные поверхности вращения пересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей (рис. 226).

В частном случае, если одна из поверхностей вращения - сфера, приведенное выше предложение может быть сформулировано иначе: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей (рис. 227).

Если ось поверхности вращения перпендикулярна плоскости проекции π₁ (или π₂ ), то окружности проецируются на плоскость π₁ (или π₂) без искажения, а на плоскость π₂ (или π₁) в отрезки прямых, перпендикулярных фронтальной (горизонтальной) проекции оси вращения (см. рис. 226).

Поверхность сферы может пересекаться по окружности не только с соосной поверхностью вращения, но и с любой другой поверхностью, имеющей семейство окружностей, например, с циклической поверхностью, конической поверхностью второго порядка, имеющей в основании окружность, и др.

Построить линии пересечения поверхностей с помощью вспомогательных секущих сфер можно двумя способами:

1) способом концентрических сфер;

2) способом эксцентрических сфер.

Особенности каждого из этих способов и условия его применения проследим на конкретных примерах.

1. Способ концентрических сфер.

Этот способ применяется для построения линии пересечения двух поверхностей вращения, оси которых пересекаются. Для упрощения графического решения необходимо, чтобы плоскость, определяемая осями поверхностей вращения, была параллельной какой-либо плоскости проекции.

ПРИМЕР 1. Построить линию пересечении двух конических поверхностей вращения с пересекающимися осями (рис. 228).

РЕШЕНИЕ.

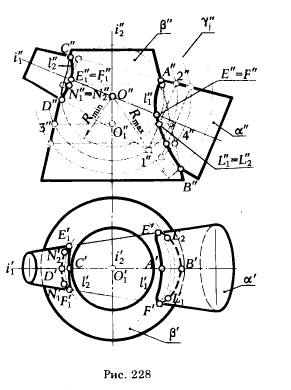
Сфера, проведенная из точки О" пересечения фронтальных проекций осей поверхностей вращения, пересечет поверхность α по окружности, которая проецируется на плоскость π₂ в отрезок [1"2"], а поверхность β - по окружности, проецирующейся на π₂ в отрезок [ 3"4"]. На горизонтальную плоскость проекции эта окружность спроецируетсн без искажения в окружность радиуса |О"₁, 3"|, проведенную из центра в точке О'.

Пересечение отрезков [1"2"] и [3"4"] укажет фронтальные проекции двух точек L"₁ и L"₂(L"₁ ≡ L₂"), принадлежащих линии пересечения поверхностей α и β. Величина радиуса вспомогательных сфер для определения линии l₁ изменяется в пределах от R_min = |0"M"| дo R_max = |0"В"| (точка М" определяется как точка касания окружности, проведенной к главному меридиану поверхности β из центра О"). Для определения точек линии l₂ R_max = |0"С"|, R_min = |0"М"|. На рис. 228 показано определение точек N"₁ и N"₂, принадлежащих линии l₂. Горизонтальная проекция линии пересечения может быть найдена из условия ее принадлежности поверхности β. Для ее построения необходимо через фронтальные проекции точек кривых l"₁ и l"₂ провести горизонтальные прямые - фронтальные проекции параллелей поверхности β, а из точки O' - окружности - горизонтальные проекции параллелей, на которых с помощью линий связи можно определить горизонтальные проекции точек, принадлежащих кривым l'₁ и l'₂ Особые точки A, В, C, D определяются пересечением главных меридианов поверхностей α и β. Они же являются высшими (точки A и С) и низшими (точки В и D) точками линии пересечения поверхностей. Границы видимости линии на горизонтальной плоскости проекции определяются точками, принадлежащими горизонтальному очерку поверхности α ( точки Е'₁ и E'₂ для линии l₂ и F'₁ и F'₂ для линии l₁ ] ).

ПРИМЕР 2. Построить линию пересечения поверхности вращения а произвольного вида с поверхностью прямого кругового цилиндра β. Оси поверхностей пересекаются (рис. 229) .

РЕШЕНИЕ.

1. Определяем центр вспомогательных сфер - точку пересечения осей поверхностей вращения О = i₁ ∩ i₂ .

2. Находим проекции опорных точек, принадлежащие линии пересечения l (А", В", С", D"). Так как эти точки принадлежат плоскости главных меридианов поверхностей, которая параллельна плоскости π₂, то эти точки определяются пересечением фронтальных проекций главных меридианов поверхностей.

3. Для определения произвольных (промежуточных) точек линии пересечения из точки О" проводим семейство концентрических окружностей, являющихся фронтальными проекциями вспо-могательных сфер.

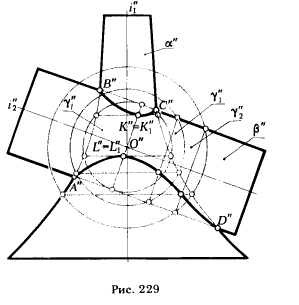
Радиус максимальной сферы равен расстоянию от фронтальной проекции центра сферы О" до наиболее удаленной проекции точки, принадлежащей линии пересечения - точки D". Величина минимального радиуса вспомогательной секущей сферы равна радиусу окружности, касающейся цилиндра β". На рис. 229 показано построение точек К, К₁ и L, L₁ с помощью вспомогательной сферы γ_j.

Горизонтальные проекции точек линии пересечения строятся при помощи параллелей поверхности вращения α, которые проецируются на плоскость π₁ без искажения.

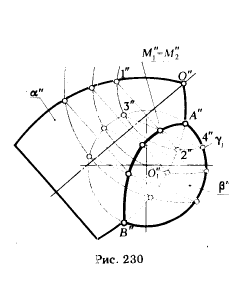
ПРИМЕР 3. Построить линию пересечения поверхности тора α и сферы β, оси которых определяют плоскость, параллельную фронтальной плоскости проекции (рис. 230) .

РЕШЕНИЕ.

Так как осью сферической поверхности может быть любая прямая, проходящая через центр этой поверхности, то за центр вспомогательных сферических поверхностей можно принять произвольную точку на оси поверхности вращения α. Поэтому графическое решение задачи по определению линии пересечения заданных поверхностей сводится к выполнению следующих геометрических построений :

1. Принимаем точку О" за центр окружностей - фронтальных проекций вспомогательных секущих сфер.

2. Проводим фронтальную проекцию вспомогательной сферической поверхности γ_j.

3. Определяем отрезки [ 1"2"] и [ 3"4" ] - фронтальные проекции окружностей, по которым γ_j∩ α и γ_j ∩ β.

4. Точки пересечения окружностей (отрезков [1"2"] и [3"4"] ) M"₁ и М"₂ принадлежат искомой линии пересечения.

5. Фронтальные проекции опорных точек А" и В" определяются пересечением фронтальных проекций меридианов поверхностей α и β.

6. Горизонтальные проекции линии пересечения определяются с помощью параллелей поверхности β.

2. Способ эксцентрических сфер.

Способ эксцентрических сфер может быть использован для построения линии пересечения двух поверхностей, имеющих общую плоскость симметрии. При этом каждая поверхность должна иметь семейство окружностей. Как и в способе концентрических сфер, плоскость симметрии должна быть параллельна одной из плоскостей проекции. Сущность способа легко уяснить из следующих примеров.

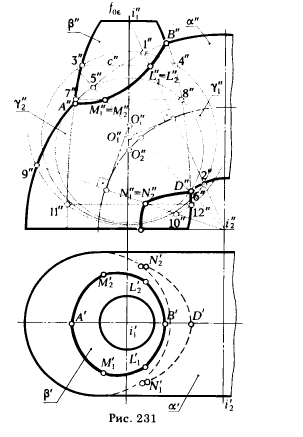
ПРИМЕР 1. Построить линию пересечения поверхности кольца (открытого тора) а с поверхностью вращения β, имеющих общую плоскость симметрии (рис. 231).

РЕШЕНИЕ.

Хотя мы и имеем дело с поверхностями вращения, но применить здесь способ концентрических сфер не представляется возможным, так как оси поверхностей не пересекаются.

Возможность использования способа эксцентрических сфер обусловливается тем, что обе поверхности несут на себе семейства окружностей, по которым они могут пересекаться эксцентрическими сферами, причем на кольцевой поверхности имеется несколько семейств окружностей, в том числе и окружностей, принадлежащих пучку плоскостей, ось которого совпадает с осью кольца.

Решение задачи сводится к следующим графическим построениям:

1. Рассечем кольцевую поверхность фронтально проецирующей плоскостью ε, проходящей через ось кольца; эта плос кость пересечет кольцевую поверхность по окружности, фронтальная проекция которой - отрезок [1"2"]. Эта же окружность может быть получена, если кольцевую поверхность пересекать семейством эксцентрических сфер, центры которых расположены на перпендикуляре, проведенном через центр окружности к плоскости ε.

Для того чтобы вспомогательная сфера пересекала по окружности и поверхность вращения β, необходимо, чтобы ее центр принадлежал оси этой поверхности. Поэтому за центр вспомогательной сферы следует брать точку О ₁ пересечения упомянутого перпендикуляра с осью поверхности β. В этом случае сфера, радиус которой равен расстоянию от точки O₁ до точки 1, пересекает обе поверхности по окружностям. Окружность с, по которой сфера пересекает поверхность β, является параллелью поверхности β; эта параллель проецируется на плоскость в отрезок [3"4"]. Окружности 1", 2" и 3", 4" пересекаются в точках L"₁ и L"₂ (L"₁ ≡ L"₂). Аналогично строятся и другие произвольные точки, принадлежащие искомой линии пересечения поверхностей α и β.

Фронтальные проекции опорных точек А" и В" определяются пересечением фронтальных проекций главных меридианов поверхностей α и β. Горизонтальные проекции (на рис. 231 не показаны) могут быть построены с помощью параллелей поверхности β так же, как это было сделано в примере 2.

Способ эксцентрических сфер можно применять и в тех случаях, когда одна из пересекающихся поверхностей не является поверхностью вращения. Необходимым условием является наличие на этой поверхности семейства окружностей, которые можно рассматривать как результат пересечения поверхности со сферой. В число условий входит также условие, чтобы перпендикуляры, восставленные из центров круговых сечений, пересекали ось поверхности вращения.

Задача, помещенная в следующем примере, иллюстрирует возможность использования эксцентрических сфер для построения линии пересечения двух поверхностей, когда одна из них не является поверхностью вращения.

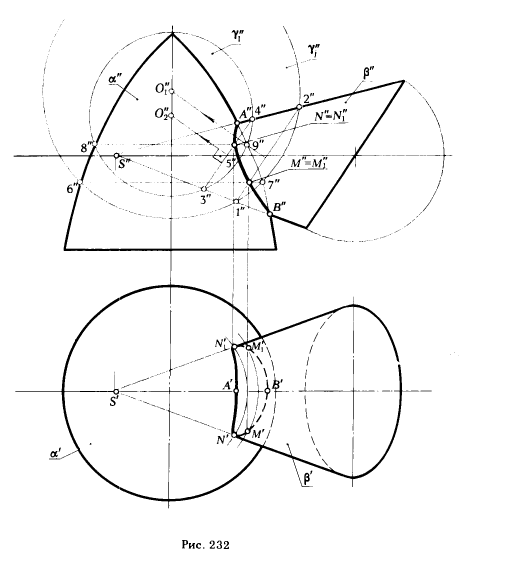
ПРИМЕР 2. Построить линию пересечения поверхности вращения α с конической поверхностью второго порядка β, имеющей в основании окружность (рис. 232).

РЕШЕНИЕ.

1. Выделим на конической поверхности β круговое сечение. Для этого пересечем поверхность β фронтально проецирующей плоскостью, параллельной основанию конуса. Эта плоскость пересечет коническую поверхность по окружности, которая проецируется на фронтальную плоскость проекции в виде отрезка [1"2"].

Перпендикуляр, восставленный из центра этой окружности к ее плоскости, пересечет ось поверхности вращения в точке O₁, которую принимаем за центр вспомогательной секущей сферы γ_j. Центр другой эксцентрической сферы γ_j можно определить аналогично рассмотренному случаю. Построения начинаем с проведения прямой (3"4"), параллельной прямой (1 "2"); из точки 5" (середины отрезка [3"4"]) восставляем перпендикуляр к отрезку [3"4"] и определяем точку О₂ пересечения его с осью поверхности вращения α.

3. Сферы, проведенные из центров О₁ и O₂ радиусами, соответственно равными | О"₁1"| и | O"₂3"|, пересекают по окружностям не только поверхность β, но и поверхность вращения α. Отрезки [6", 7"] и [8", 9"] являются фронтальными проекциями этих окружностей. Пересечения отрезков [ 1",2"] и [ 6",7"], [3", 4"] и [8", 9"] укажут точки M", М"₁ и N", N"₁, принадлежащие линии пересечения поверхностей α и β.

Фронтальные проекции опорных точек А" и В" определяются пересечением фронтальных проекций главных меридианов поверхностей α и β. Горизонтальные проекции точек, принадлежащих линии пересечения, определяются известным способом (см. пример 1, рис. 228).