Построение линии пересечения поверхностей (общий случай)

В алгоритме для решения задач на построение линии пересечения двух поверхностей l = (L₁ ∪ L₂ ∪ L₃ ∪ ... ∪ L_n); |(γ_j ∩ α) ∩ (γ_j ∩ β)] в качестве вспомогательной поверхности (посредника) γ_j следует выбирать поверхности, которые пересекали бы заданные поверхности α и β по наиболее простым для построения линиям - прямым или окружностям.

В качестве вспомогательных поверхностей - посредников наиболее часто используются плоскости и сферы; при решении некоторых задач бывает целесообразно обращаться за помощью к цилиндрическим и коническим поверхностям.

Ниже будет показано решение задач на определение линии пересечения поверхностей с помощью вспомогательных секущих плоскостей (§ 48), цилиндрических (§ 49), конических (§ 50), а также сферических (§ 51) поверхностей.

Прежде чем решить вопрос, какую вспомогательную секущую поверхность выбрать для построения линии пересечения поверхностей, следует выяснить, не занимает ли одна из пересекающихся поверхностей проецирующее положение, так как в данном случае решение поставленной задачи значительно упрощается. Это происходит из-за того, что одна из проекций линии пересечения будет совпадать со следом проецирующей поверхности, которая входит в условия поставленной задачи (см. инвариантное свойство 2г, § 6).

Поэтому решение сводится к определению недостающей проекции линии, принадлежащей поверхности, если известна одна ее проекция и указаны проекции поверхности (см. § 41, пример 1, рис. 178).

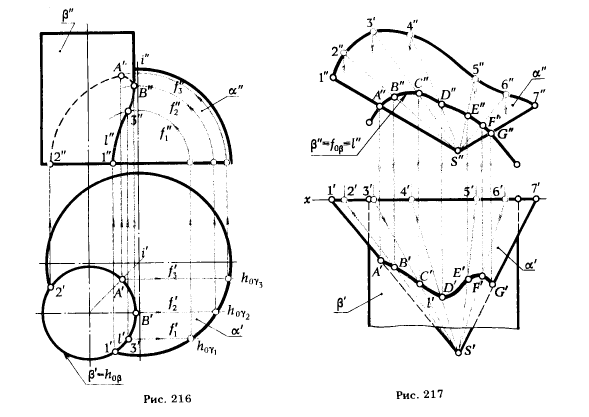
Рис. 216 иллюстрирует решение задачи по определению линии l = α ∩ β, при этом β ⊥ π₁ . Зелеными линиями показано построение фронтальной проекции l" - линии пересечения сферической поверхности α с поверхностью горизонтально проецирующего прямого кругового цилиндра β. Точка А, принадлежащая линии пересечения поверхностей и являющаяся ближайшей к вертикальной оси i поверхности сферы, одновременно будет высшей точкой А" на фронтальной проекции кривой l". Точка В" - крайняя правая на линии пересечения является также границей видимости кривой l".

На рис. 217 показано определение горизонтальной проекции l' - линии пересечения произвольной конической поверхности α с фронтально проецирующей цилиндрической поверхностью β. В этом случае, как и в предыдущем примере, задача на построение линии пересечения поверхностей сводится к определению недостающей проекции линии l, принадлежащей поверхности α. Все построения, необходимые для нахождения точек А', В', С', ... кривой l' по заданным точкам А", В", С", ..., выполнены зелеными линиями и не нуждаются в дополнительных пояснениях.